Kinderen houden van wiskundig nadenken

Regelmatig uiten mijn pabostudenten hun zorgen over leerlingen die de tafels van vermenigvuldiging steeds weer vergeten en bijvoorbeeld over kinderen die in verwarring raken als in één les aan verschillende leerdoelen wordt gewerkt. Als ik mijn studenten zo beluister, lijken basisscholen bij het vak rekenen-wiskunde steeds vaker te kiezen voor het inoefenen van vaardigheden via voordoen en nadoen (kopiëren) in plaats van het werken vanuit begrip en betekenis waarbij de kinderen ruimte krijgen om zelf na te denken (construeren). Dat de nadruk ligt op het kopiëren van strategieën is jammer, want kinderen zijn prima in staat om zelf na te denken. Sterker nog: ze houden ervan! Onderstaande ervaring laat zien hoe kinderen in staat zijn wiskundig te redeneren zonder dat de leerkracht het voorleeft. Ook is er alle ruimte voor het ontwikkelen van een wiskundige attitude en plezier in het vak. Het vraagstuk is afkomstig uit een artikel over probleemoplossen van Van Zanten (2019).

Welke hoort er niet bij?

In groep 8 van de Julianaschool in Bilthoven leg ik aan de leerlingen het denkvierkant van figuur 1 voor en vraag ze welk getal er volgens hen niet bij hoort. Voordat de leerlingen losbarsten met hun ideeën, praten we over wat wiskunde eigenlijk is en hoe een wiskundige te werk gaat. We concluderen dat een wiskundige geïnteresseerd is in de manieren waarop je tot een antwoord kunt komen en dat de weg naar een antwoord toe eigenlijk veel interessanter is dan het antwoord zelf. Ik voeg eraan toe dat een wiskundige steeds weer blijft zoeken naar nieuwe, nóg mooiere oplossingen. Vandaag oefenen de leerlingen met die attitude. Ze nemen geen genoegen met één antwoord en proberen te begrijpen hoe klasgenoten hebben geredeneerd. Ook vergelijken ze hun eigen denkwijze met die van anderen.

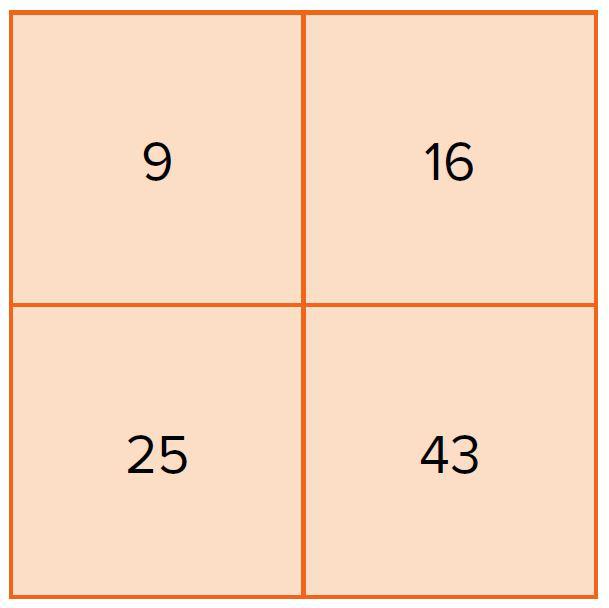
Matthijs denkt dat 16 er niet bij hoort, want dit is het enige getal dat in de tafel van vier voorkomt. Hij heeft ook nog een ander idee, namelijk 43 als buitenstaander. Met de drie andere getallen kun je namelijk een som maken; 9+16=25. Siem reageert op de denkwijze van Matthijs. Hij heeft ook 16 gekozen als getal dat er niet bij hoort, maar om een andere reden. 16 is namelijk als enige van de vier getallen een even getal. Als mijn vraag luidt: ‘Wie heeft een oplossing bedacht die anderen waarschijnlijk niet hebben opgeschreven?’, komen er nog meer ideeën bij de kinderen los. Ik zie klasgenoten naar het puntje van hun stoel schuiven. Philip heeft gekozen voor het getal 9. Dit is namelijk het enige getal waarvoor niet geldt dat het bij vermenigvuldigen met zeven boven de 100 uitkomt. Ik kijk de klas rond; er is niemand die dit ook had bedacht. Philip denkt nog zo’n unieke te hebben gevonden. 25 hoort er volgens hem niet bij, omdat het bij verdubbelen tot een rond getal leidt, een tiental. Dat is bij de andere drie getallen niet het geval. Er zijn enkele kinderen die dit idee ook hebben opgeschreven. Met het getal 25 kunnen we nog even doorgaan: het is het enige getal dat deelbaar is door 5 en het heeft als enige van de getallen geen eenheden die deelbaar zijn door 3. Noa vermoedt dat zij iets heeft gevonden dat voor klasgenoten een verrassing kan zijn. 25 is namelijk het enige getal dat geen gesloten cijfersymbool kent; ‘dat niet dicht zit’, zoals zij het zelf verwoordt. De 9, de 6 en de 4 zijn een gesloten cijfersymbool. Niemand had dit nog ontdekt. Er zijn meer ideeën die aandacht verdienen, maar Wisse mag afsluiten. Hij heeft 43 gekozen als getal dat er niet bij hoort, omdat het een priemgetal is en de rest niet. Lex wil graag weten wat Wisse daarmee bedoelt. Hij heeft nog niet eerder van een priemgetal gehoord.

De kracht van het denkvierkant

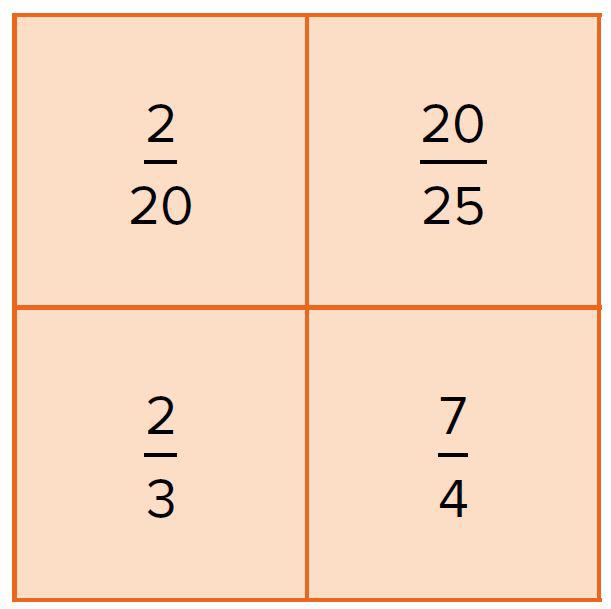
Dit vraagstuk nodigt niet alleen uit tot het zelf construeren van een oplossing, maar ook tot doorzetten en verder zoeken, het stimuleert eveneens tot luisteren, leren van elkaar en tot gebruik van wiskundetaal. Even getallen, tiental, priemgetal, cijfersymbool en eenheden zijn wiskundige termen die tijdens het interactieve gesprek naar voren komen. Bij figuur 2 gebeurde hetzelfde toen ik de vraag stelde welke breuk er niet bij hoort.

2/3 heeft als enige een noemer die deelbaar is door 3; 3/20 is als enige te vereenvoudigen tot een stambreuk en 2/3 is als enige een repeterende breuk.

Een simpel wiskundig probleem, zo lijkt het, maar met zoveel verschillende manieren om ernaar te kijken. Daardoor is er ook ruimte voor het wiskundig denken van álle leerlingen; van zwak tot sterk in rekenen-wiskunde.

Wiskundige attitude

De leerlingen van groep 8 van de Julianaschool laten niet alleen zien plezier te beleven aan het wiskundig denken, maar ze overtuigen mij er ook van over een wiskundige attitude te beschikken (Oonk & De Goeij, 2006; De Goeij & Oonk, 2017). Ze stellen zich onderzoekend op en zijn benieuwd naar andere mogelijke redeneringen, ze proberen in te schatten of hun eigen oplossing uniek zal zijn of door meerdere kinderen is gevonden. Dit vraagt om reflectie op de wiskundige inhoud: Wat weet ik van dit onderwerp? Heb ik iets gevonden dat tot makkelijke of moeilijke wiskunde-inhoud behoort? Is het onderwerp vaak aan de orde geweest of niet?

Doorzettingsvermogen, zelfvertrouwen en plezier vallen onder de algemene wiskundige attitude. En het gesprek over het wiskundig redeneren is een voorbeeld van een activiteit waarbij de leerlingen hun communicatieve houding aanspreken. Zo zijn er verschillende categorieën van wiskundige attitudes waarvoor denkvierkanten ruimte bieden.

Hoe stimuleer je wiskundig nadenken?

De kracht zit niet alleen in het wiskundige vraagstuk zelf. Wat kinderen ook nodig hebben om tot wiskundig denken te komen, is een leerkracht die denkvragen stelt, die ruimte geeft voor het eigen denken en oprecht geïnteresseerd is in nieuwe oplossingen die kinderen aandragen. Een leerkracht die vervolgens uitnodigt tot reflectie. Dit keer was in groep 8 de reflectie gericht op attitude. Nadat de leerlingen ook zelf denkvierkanten hebben gemaakt, blikken we terug op ons startgesprek. Wat leerde je van dit vraagstuk en wat bracht het jou om als wiskundige te denken? Angelina schrijft: ‘Ik heb geleerd verder te kijken dan mijn neus lang is’. Daarmee bedoelt ze dat ze van haar medeleerlingen heeft geleerd op een andere manier naar het denkvierkant te kijken. Noa leerde dat er veel verbanden zijn tussen getallen. Meerdere kinderen benadrukken het doorzetten en de diversiteit in oplossingen:

Mijn eigen nieuwsgierigheid leidde ertoe dat ik de kinderen vroeg om een unieke oplossing. Met deze vraag draag ik mijn nieuwsgierigheid over op de kinderen. En het plezier dat je zelf als leerkracht ervaart tijdens het wiskundig redeneren werkt ook aanstekelijk. Met andere woorden, de winst zit ‘m vooral in het voorleven van een wiskundige attitude. Veel meer dan in het voorleven van een oplossingsstrategie of een antwoord.

Naast voorleven van een wiskundige attitude is ook het hanteren van de drie-seconden-regel een leerkrachtvaardigheid waarmee je wiskundig denken stimuleert. Rowe (1986) stelt dat drie seconden pauzeren na het stellen van een vraag aan de groep en drie seconden wachten na de reactie van een leerling meerdere positieve effecten heeft. Zo gaan leerlingen uitgebreider antwoorden en gebruiken ze daarbij vaak ook meer argumenten. Ook gaan leerlingen eerder zelf een vraag inbrengen als in de interactie meer denktijd wordt gecreëerd. Ze raken meer betrokken bij elkaars inbreng; horizontale interactie komt tot stand en het gesprek raakt minder gecentreerd rondom de leerkracht. Ook groeit de diversiteit in de reacties, omdat meer kinderen gaan deelnemen aan het interactieve gesprek.

Tot slot

Wat word ik blij van de kinderen die in dit artikel aan het woord kwamen: ze denken na als jonge wiskundigen, maken hun eigen constructies en wisselen die uit met anderen. Ze ontwikkelen een wiskundige attitude die hen niet alleen brengt tot een hoger niveau van wiskundig denken, maar die in de toekomst ook breder inzetbaar is. Met doorzettingsvermogen, vaktaal, plezier in leren, een onderzoekende en reflectieve houding leren kinderen voor het leven en vergeten ze niet zomaar wat ze eerder hebben geleerd.