Rekenen-wiskunde is en blijft een uitdagend gesprek

Vele jaren geleden vroeg ik me als jonge leerkracht af waarom ik soms met een klas vol vaag kijkende gezichten werd geconfronteerd. Ik had de kinderen de vraag gesteld om zich een rekenles van vorige week of zelfs de dag ervoor te herinneren. Mijn les was dus niet blijven hangen. Hadden de kinderen dan helemaal niets geleerd, had ik dan geen goed reken-wiskundig gesprek gevoerd?

 

Rekenen-wiskunde – het gesprek

Denken en communiceren zijn twee kanten van dezelfde medaille; we communiceren op de manier waarop we denken en denken op de manier waarop we communiceren. Ons denken is in feite communicatie met onszelf (Sfard, 2009).

Reken-wiskundig denken is een uitdagende dialoog die mensen al duizenden jaren met elkaar voeren - een gesprek over de relatie tussen dingen. Dit gesprek gaat vaak over de relaties tussen hoeveelheden en over de relatie tussen de dingen onderling (zoals vormen of gebeurtenissen, bijvoorbeeld de overgang tussen dag en nacht). Wij mensen hebben getalsymbolen, strategieën, algoritmen en maten in allerlei soorten uitgevonden om ons hierbij te helpen.
Het is de taak van de leerkracht om kinderen uit te dagen om mee te doen aan dit reken-wiskundig gesprek. Bij zo’n gesprek gaat het om veel meer dan woorden alleen. Concreet materiaal, tekeningen, schema's en afbeeldingen, evenals een toenemend aantal symbolen horen hier ook bij.

 

Leren om aan het gesprek mee te doen

Zodra kinderen geboren worden, zijn hoeveelheden in allerlei soorten en maten van groot belang: 'genoeg' en 'niet genoeg', 'te heet' en 'te koud' zijn ervaringen waar kleine kinderen direct en vaak luid op reageren. Tijdens hun vroege ontwikkeling blijven kinderen aandacht besteden aan hoeveelheden, zowel om hun eigen behoeften te bevredigen als uit pure nieuwsgierigheid. Relaties tussen hoeveelheden zoals 'meer', 'groter' en 'kleiner' vinden ze erg belangrijk, zeker binnen het gezin en de eigen groep. Alle kinderen beginnen lang voordat ze naar school gaan al met rekenen-wiskunde. Ze doen hun uiterste best om met anderen te communiceren over hoeveelheden en over de relaties tussen aantallen.

Normaal gesproken worden jonge kinderen al aangemoedigd door hun omgeving om te tellen voordat ze naar school gaan. Dit gebeurt meer omdat wij als volwassenen ze daartoe uitnodigen, niet omdat kunnen tellen tegemoetkomt aan een of andere praktische behoefte van henzelf. In feite hebben jonge kinderen als ze leren tellen absoluut geen idee waarom ze dat gevraagd wordt. Het is simpelweg een sociale prestatie die door anderen rond hen heen gewaardeerd wordt en het nut ervan blijft nog een verrassend lange periode een compleet mysterie. Jonge kinderen doen mee met telrituelen om ons en zichzelf een plezier te doen, niet omdat het eventuele praktische problemen die ze tegenkomen helpt oplossen. Langzamerhand beginnen kinderen echter hun praktische ervaring met aantallen en de gesprekken hierover te verbinden met de telwoorden en symbolen die we bij het tellen gebruiken, wanneer ze zich gaan realiseren dat deze woorden en symbolen te maken kunnen hebben met de grootte van de verzamelingen.

De één-één-relatie is een belangrijke relatie die kinderen helpt zich te realiseren dat tellen met aantallen te maken heeft. Twee verzamelingen voorwerpen hebben dezelfde 'grootte' in aantal als de voorwerpen in die verzamelingen in een één-één-relatie ten opzichte van elkaar kunnen worden gezet. Als dat niet mogelijk is, dan is de ene verzameling getalsmatig (in aantal) groter dan de andere. Vaak leren kinderen eerst de relevantie van de hoeveelheid in de één-één-relatie in situaties waar gedeeld moet worden ('één voor mij, één voor jou, ...') en bijvoorbeeld bij rituelen als tafeldekken. Geleidelijk leren kinderen met ons te communiceren over hoe de grootte van verzamelingen en hoeveelheden met elkaar te maken hebben. Vervolgens verbinden zij deze communicatie over hoeveelheden met het sociale ritueel van tellen. Dit stelt kinderen in staat mee te doen met het grote gesprek dat we rekenen-wiskunde noemen.

 

Ontdekken, leren verbeelden en leren praten over

Getallenlijnen, het rekenontwikkelingsmateriaal, de Numicon-vormen, en de Cuisenaire-staafjes zijn ontwikkeld om de communicatie van kinderen over relaties tussen dingen en aantallen te ondersteunen.

Cognitief psycholoog Daniel Willingham (2013) beschrijft deze concrete materialen als een 'metafoor voor het abstracte'. Hij legt ook uit dat het materiaal zelf ook abstract is wanneer kinderen er voor het eerst kennis mee maken. Het is van belang dat we kinderen voldoende tijd geven om vertrouwd te raken met de rekenmaterialen die we hen geven. We moeten ze de ruimte geven om te ontdekken dat deze materialen representaties zijn van hoeveelheden. Deze kennismaking zit achter Gattegno's (2010) wijze advies om kinderen te laten spelen met deze materialen voordat ze proberen er abstracte sommen mee te maken.

Het was Bruner (1966) die de termen enactive, iconic en symbolic invoerde om de ontwikkelingsstadia in het leerproces (van concreet naar abstract) te beschrijven en grip te krijgen op nieuwe concepten. De enactive-fase, het informeel handelen (Van Groenestijn, Borghouts & Janssen, 2011) is de belangrijkste, het is de fundering. Dit is de natuurlijke weg van ontdekken: letterlijk actief zijn, het manipuleren van materialen om ons heen. In de iconic-fase, het voorstellen, ontwikkelen kinderen, vaak simultaan aan de vorige fase, beelden van de dingen die zij hebben ervaren. Een kind heeft bijvoorbeeld gereisd met een bus en herkent een plaatje of pictogram van een bus. Deze afbeelding van een bus kan er totaal anders uitzien dan de bus waarin gereisd is, toch is het een ‘bus’. Hierna kan in de symbolic-fase, het formeel handelen, het woord ‘bus’ geschreven worden. Ondanks dat de letters totaal niet lijken op het plaatje van een bus, weet het kind dat beide hetzelfde representeren.

Dit is natuurlijk ook zo bij getallen. Het getal vier op een dobbelsteen, afgebeeld als vier stippen op de hoekpunten van een vierkant, is iconic van dat wat geïnterpreteerd kan worden als ‘vier’ bij het tellen. Het cijfer 4 daarentegen lijkt niet op de vier stippen. Zonder de voorkennis dat we het cijfer 4 willekeurig hebben toegewezen aan de hoeveelheid vier, zou het niet als hoeveelheid vier gezien worden (Van Doesburg, de Rooij & van Schie, 2020). De drie fasen van Bruner vormen ook de kern van het werken met Numicon. Hieronder beschrijven we een voorbeeld van het aanleren van de abstracte begrippen even en oneven.

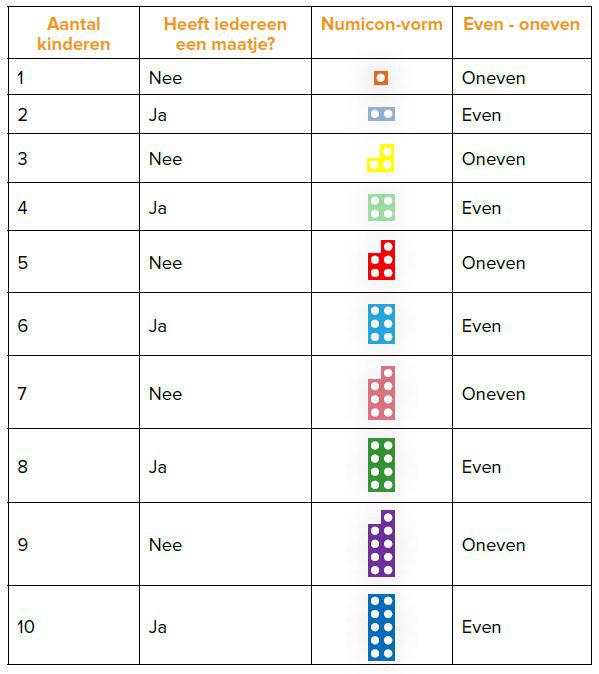
• Informeel handelen: kinderen worden gevraagd om letterlijk een maatje te zoeken om in de bus naast te gaan zitten. De vraag wordt gesteld of dit lukt bij 10 kinderen, maar lukt dit ook bij bijvoorbeeld 9 kinderen en bij 8 en bij 7 etc.?  Bespreek met de kinderen wat opvalt en zet de bevindingen in een schema.
• Voorstellen: kinderen doen ervaring op in de volgende opdracht. Ze worden gevraagd om de afbeeldingen van de Numicon-vormen te gebruiken om de begrippen even en oneven te onderzoeken. Kinderen ontdekken dat bij een aantal vormen de 2 twee rijtjes niet even lang zijn, ze zijn ongelijk. Dus zijn ze oneven.
  Door deze activiteit worden kinderen aangemoedigd om de Numicon-vormen te gebruiken om hun bevindingen in een tabel (zie afbeelding 3) te zetten en ze tevens te vergelijken met de resultaten van de vorige activiteit.
• Formeel handelen: Ten slotte, als kinderen een abstract beeld van een getal ontwikkelen (bijvoorbeeld de Numicon-vorm of een dobbelsteenpatroon), kunnen ze een begin maken met het leren verbeelden. Zodat wanneer ze de afbeelding zien, ze meteen weten welk getal erbij hoort. De volgende vragen zou je hierbij kunnen stellen:

-          Is het antwoord ‘even’ of ‘oneven’ bij een optelling van een even getal plus een even getal?;

-          Hoe is dit als je een even getal plus een oneven getal optelt?

-          Wat als je twee oneven getallen bij elkaar optelt?

-          En hoe is dit bij de eraf-bewerking?

 

De opbouw in deze activiteiten is een voorbeeld van leren van concreet naar abstract. In eerste instantie wordt kinderen gevraagd om zichzelf in paren te rangschikken (concreet en laagste handelingsniveau); dit is passend bij de belevingswereld van het kind. Hierna ontdekken de kinderen dat je even en oneven kan modelleren met Numicon-vormen (als afbeelding). En ten slotte introduceren ze geschreven cijfers (abstract).

Het uiteindelijke doel van het werken met concrete materialen is om het materiaal overbodig te maken. Dat wil zeggen, we gebruiken concreet materiaal totdat we het niet langer hoeven te gebruiken. Het is cruciaal om kinderen voldoende tijd te geven om te manipuleren en verwoorden van wat we spelenderwijs, handelend en ontdekkend opmerken over deze materialen. Dit stimuleert kinderen om na te denken over rekenwiskundige concepten.

Het gegeven voorbeeld laat zien dat kinderen na het ontdekken van de gelijke en ongelijke vormen de generalisatie kunnen maken dat de ongelijke vormen altijd oneven zijn. En dat het aantal, het getal, die deze vorm representeert dus ook oneven is. Generaliseren van ervaringen die kinderen opdoen tijdens allerlei rekenwiskundige situaties, begint al op zeer jonge leeftijd.  

 

Generaliseren - het begint eerder dan je denkt

Al vroeg in het leven van een kind hoort het oudere mensen over abstracte dingen praten. Het kind wil graag meedoen. Wij, als volwassenen, willen ook dat kinderen meedoen: we willen dat zij met ons praten over dingen die getallen heten. Het probleem is dat getallen abstract zijn en ze niet echt bestaan zoals tastbare dingen dat wel doen. Je kan getallen niet zien, aanraken of proeven. Getallen zijn geen echte materiële zaken - het zijn generalisaties.
Op enig moment in onze gesprekken met kinderen beginnen we telwoorden als zelfstandig naamwoorden te gebruiken. We praten over 'vijf' als een op zichzelf staand ding, in plaats van vijf potloden of stoelen, of over 'vijf jaar oud zijn' (hoewel we, lekker verwarrend, ook vaak dingen zeggen als ‘Jij bent vijf’, alsof het kind zelf een getal is). Als we op deze manier over 'vijf' praten bedoelen we 'vijf van iets'. Zo proberen we kinderen te laten generaliseren.
Als we kinderen een bewerking zoals ‘3 + 4 = 7’ laten zien, willen we ook dat zij dit begrijpen als een generalisatie. We gebruiken deze bewerking om te zeggen dat 'drie van iets opgeteld bij vier van iets  samen zeven iets zijn'. We generaliseren en wat belangrijk is: we voorspellen. Dat is voor kinderen echt een grote stap.

 

Reken-wiskundig denken houdt ook in dat er een verbinding gelegd moet worden tussen de (abstracte) rekenwiskundige generalisaties en het alledaagse. Dit betekent dat kinderen niet alleen leren hoe en wat ze kunnen doen met rekenen-wiskunde, maar ook wanneer dit geschikt is. Graag willen we de kinderen leren rekenen in alledaagse situaties. In gegeven en bedachte contexten, zodat kinderen leren redeneren. Bijvoorbeeld bij een redactiesom, waarbij je eerst de relevante informatie moet filteren, daarna een passende oplossingsstrategie moet bedenken en vervolgens deze correct uitvoeren.

 

Leren communiceren over generalisaties met materialen - variatie en regelmatigheid

Een manier om kinderen te helpen generaliseren is hen variatie te bieden in hun ervaringen en situaties aan te reiken van waaruit ze kunnen generaliseren. Als we de leerstof maar op één manier aanbieden, wordt het erg moeilijk voor kinderen om gemeenschappelijkheden binnen een serie situaties te ontdekken. Dit geldt ook voor het leren werken met hoeveelheden. Daarom nodigen we kinderen uit om te werken met zoveel mogelijk verschillende tastbare voorwerpen zoals kralen, fiches, diverse telmaterialen, Numicon-vormen, Cuisenaire-staafjes, et cetera.
De tweede manier om kinderen te helpen generaliseren is door patronen te bieden, zodat ze kunnen generaliseren over de regelmaat en de onderlinge relaties die binnen de rekenen-wiskunde zo belangrijk zijn. Zie het hiervoor genoemde voorbeeld over de abstracte begrippen even en oneven. De relaties zijn veel gemakkelijker te voelen, te laten zien en te illustreren met materialen die een regelmatige opbouw hebben; het is heel moeilijk om te zien dat 9 één groter is dan 8 als we bijvoorbeeld alleen een losse verzameling kralen of symbolen hebben om naar te kijken. Daarom concentreren we ons in het bijzonder op het gebruik van gestructureerde rekenmaterialen en het bieden van structuur in situaties die oorspronkelijk onregelmatig zijn, bijvoorbeeld door het ordenen van willekeurige reeksen in regelmatige patronen.

 

Tot slot

Het reken-wiskundig gesprek valt of staat bij de verwondering die kinderen ervaren in het dagelijks leven. Dit moeten wij als volwassenen stimuleren. We moeten er in ons onderwijs actief gebruik van maken.  Het geeft houvast en rust in het hoofd wanneer men in staat is om te denken en praten over de ontdekte patronen. Dit denken en praten over is de communicatie met onszelf: het gesprek.
Door jong met kinderen het uitdagende gesprek van rekenen-wiskunde aan te gaan, kunnen ze een stevig reken-wiskundig fundament leggen, waardoor kinderen in staat zijn om zich verder te ontwikkelen. Daardoor hebben ze geleerd te redeneren.
Wees actief met kinderen: onderzoek, praat en: generaliseer!