Het bevorderen van algebraïsch redeneren in het reken-wiskundeonderwijs op de basisschool

Inleiding

Algebra maakt in Nederland geen onderdeel uit van het reken-wiskundecurriculum van het basisonderwijs. Dit is een gemiste kans, want er is veel bewijs dat kinderen in de basisschoolleeftijd in staat zijn om algebraïsch te redeneren, zoals het redeneren over relaties tussen onbekenden (Blanton et al., 2015; Brizuela & Schliemann, 2004; Kaput et al., 2008; Van den Heuvel-Panhuizen et al., 2013). Door leerlingen al op de basisschool activiteiten aan te bieden waarin algebraïsch redeneren een rol speelt, kan mogelijk een betere basis gelegd worden voor begrip van de formele algebra die leerlingen in latere klassen (in het voortgezet onderwijs) onderwezen krijgen. Algebraïsch redeneren vraagt om bepaalde hogere-orde denkvaardigheden (HOV), zoals het redeneren over en het analyseren van relaties, het leggen van verbanden en het oplossen van problemen. Er is steeds meer aandacht voor de ontwikkeling van deze HOV – die ook wel 21e-eeuwse vaardigheden worden genoemd (Thijs et al., 2014) – binnen het onderwijs. Dit is ook zo binnen het reken-wiskundeonderwijs (curriculum.nu, 2019). Het opnemen van algebra in het reken-wiskundecurriculum van het basisonderwijs biedt mogelijk aanknopingspunten voor het stimuleren van de HOV van basisschoolleerlingen.

 

Het doel van mijn promotieonderzoek (Otten, 2020) was om inzicht te krijgen in of, hoe en in hoeverre het algebraïsch redeneren van basisschoolleerlingen gestimuleerd kan worden. In de internationale literatuur worden activiteiten die het algebraïsch redeneren van jonge leerlingen bevorderen ook wel early algebra - activiteiten (Carraher et al., 2008) genoemd. Bij dit soort activiteiten worden rijke, betekenisvolle probleemcontexten gebruikt en wordt het natuurlijk taalgebruik van leerlingen als basis genomen om te redeneren over algebraïsche concepten en ideeën (Kaput et al., 2008). Dit ‘vroege’ algebraïsche redeneren kan plaatsvinden binnen verschillende inhoudsgebieden (Kaput et al., 2008), zoals bij (eigenschappen van) getallen of bij variabelen en functies. Bij (eigenschappen van) getallen kan gedacht worden aan problemen als: 13 + 15 = 28, hoe weet je het antwoord van 15 + 13 zonder dit uit te rekenen? Of: Hoe kan je 2 x 3 gebruiken om 4 x 3 uit te rekenen? Binnen variabelen en functies kan je denken aan problemen als: Aan één tafel kunnen vier mensen zitten; als er een tweede tafel aan wordt geschoven kunnen er zes mensen zitten. Hoeveel mensen kunnen er aan drie aaneen geschoven tafels zitten? En aan tien?

 

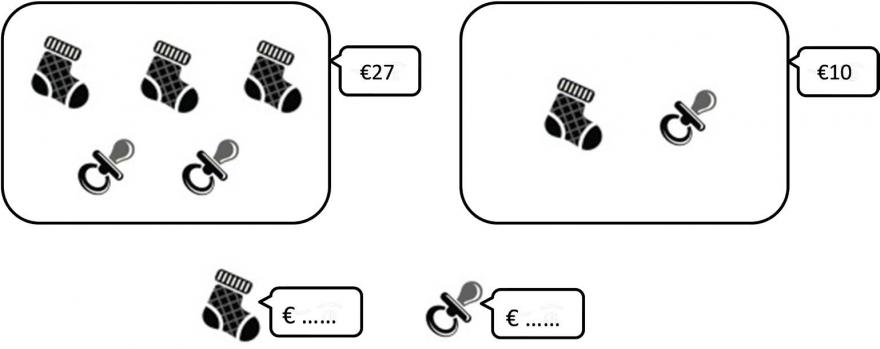
Binnen mijn promotieonderzoek hebben we ons gericht op het redeneren over vergelijkingen. Meer specifiek stond het redeneren over informele lineaire vergelijkingen centraal, oftewel, lineaire vergelijkingen die zijn weergegeven in een bepaalde context. Afbeelding 1 geeft een voorbeeld van een stelsel van twee informele lineaire vergelijkingen. In deze context-gebonden vergelijkingen is sprake van een bepaalde vorm van gelijkheid, namelijk de prijs van drie sokjes en twee speentjes is gelijk aan €27 en de prijs van één sokje en één speentje is gelijk aan €10. Door de informatie uit beide informele vergelijkingen te combineren, kan de losse prijs van één sokje en van één speentje gevonden worden.

 

De lessenserie

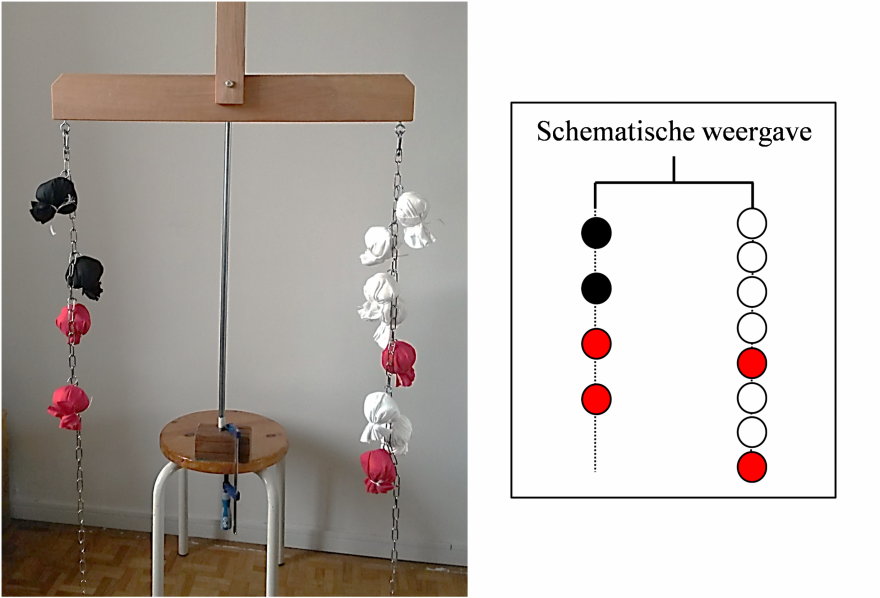
Voor ons onderzoek ontwikkelden we een zesdelige lessenserie voor leerlingen uit groep 7 over informele lineaire vergelijkingen en onderzochten we het effect van deze lessen op de ontwikkeling van hun algebraïsch redeneren. Een hangmobiel (links in afbeelding 2), oftewel een fysiek balansmodel met een horizontale balk waar aan weerszijden twee kettingen met gekleurde balletjes van verschillende gewichten hangen, stond centraal in deze lessenserie. Het balansmodel is een veelgebruikt model bij het lesgeven over lineaire vergelijkingen. Uit de eerste deelstudie van ons onderzoek, een literatuurstudie (Otten, Van den Heuvel-Panhuizen & Veldhuis, 2019), kwam onder andere naar voren dat er vele verschillende verschijningsvormen van het balansmodel zijn, zoals fysieke modellen, virtuele modellen (in een digitale omgeving), of getekende modellen, elk met andere eigenschappen. Verder bleek dat het balansmodel vooral geschikt wordt geacht om het begrip van gelijkheid in een vergelijking te bevorderen en om begrip te creëren van strategieën om deze gelijkheid te behouden, zoals hetzelfde weghalen aan beide kanten van de vergelijking. Begrip van het gelijkheidsconcept is cruciaal voor het leren oplossen van vergelijkingen (Bush & Karp, 2013; Kieran et al., 2016). Daarnaast kwam uit ons literatuuronderzoek naar voren dat precieze kennis ontbreekt over welk type balansmodel in welke situatie leidt tot de beste leeruitkomsten. Verder onderzoek bleek dus nodig om dit model optimaal in te kunnen zetten voor het leren oplossen van vergelijkingen.

 

De keuze voor de hangmobiel als specifieke vorm van een concreet balansmodel was ingegeven door een drietal redenen. Allereerst was het door de vorm van de hangmobiel mogelijk voor kinderen om de gekleurde balletjes (onbekenden in de vergelijking) fysiek te verplaatsen; hiervan verwachtten we een positief effect op de ontwikkeling van het redeneren over vergelijkingen (zie Deelstudie 3). Daarbij werd het, door gebruik te maken van kettingen waaraan de balletjes bevestigd konden worden (in plaats van in het voortgezet onderwijs meer gebruikelijke bakjes of schalen) mogelijk om de invloed van de volgorde van de balletjes op de gelijkheid in de vergelijking te zien en om die volgorde aan te passen. Tenslotte gebruikten we uitsluitend onbekenden (de gekleurde balletjes) waardoor het redeneren over de relaties tussen de onbekenden centraal stond in plaats van het vinden van de waarden van de onbekenden.

 

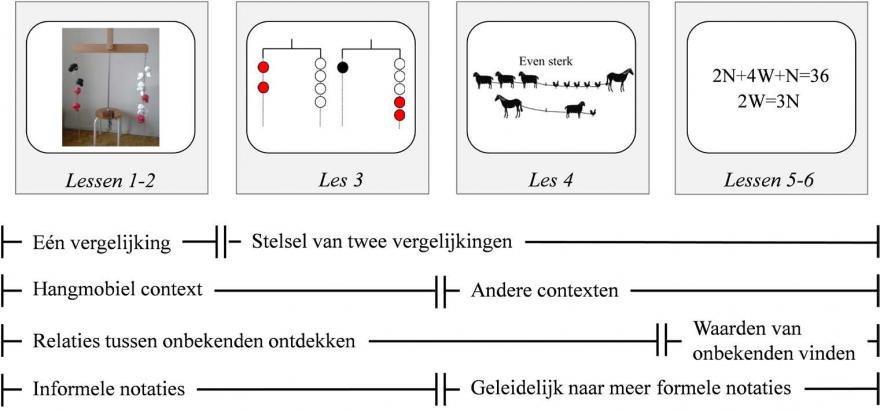
Een schematische weergave van de opbouw van onze lessenserie is te zien in afbeelding 3. In de lessenserie stond het werken met het balansmodel voornamelijk in de eerste twee lessen centraal.

De belangrijkste taak voor de leerlingen was om ‘te ontdekken wat je allemaal kan doen, terwijl je zorgt dat de hangmobiel recht blijft’. Het in balans, en dus horizontaal, houden van deze balk staat model voor het behouden van de gelijkheid in een vergelijking. Leerlingen konden verschillende handelingen uitvoeren, wat resulteerde in het al dan niet uit evenwicht brengen van de horizontale balk. Zo konden ze de volgorde van de balletjes aan één kant van de hangmobiel veranderen (ook wel: herstructureren), balletjes met gelijke kleuren aan beide kanten weghalen (ook wel: isoleren), of balletjes van één kleur vervangen door balletjes van een andere kleur (ook wel: substitueren). Tijdens het werken met de hangmobiel konden leerlingen op een intuïtieve manier informele algebraïsche strategieën toepassen en ontwikkelen waarbij de gelijkheid in een vergelijking behouden bleef. Deze context-gebonden algebraïsche strategieën liggen ten grondslag aan conventionele strategieën voor het oplossen van lineaire vergelijkingen. De verwachting was dat de fysieke ervaringen met het model zouden bijdragen aan het ontwikkelen van begrip van het concept gelijkheid en strategieën om deze gelijkheid te behouden. Het idee dat fysieke ervaringen waardevol zijn voor het begrijpen van abstracte ideeën, zoals wiskundige concepten, komt terug in theorieën over embodied cognition (vertaling: belichaamde cognitie, Gallese & Lakoff, 2005; Lakoff & Johnson, 1980; Núñez et al., 1999; Wilson, 2002).

 

Door leerlingen met het balansmodel te laten werken, beoogden we een basis mee te geven voor het oplossen van vergelijkingen (één vergelijking of een stelsel van twee vergelijkingen) in verschillende contexten (afbeelding 3, lessen 3 en 4), en uiteindelijk zelfs voor het oplossen van stelsels van vergelijkingen met formele symbolen (afbeelding 3, lessen 5 en 6). Het oplossen van stelsels van vergelijkingen vraagt om geavanceerde algebraïsche vaardigheden, zoals het redeneren over relaties tussen onbekenden in vergelijkingen, het redeneren over onderlinge relaties tussen vergelijkingen, het manipuleren van deze relaties, het combineren ervan en het redeneren op basis van deze nieuwverworven informatie. Dit soort vaardigheden wordt ook wel gezien als een belangrijk aspect van wiskundige HOV. Het redeneren over informele vergelijkingen, waarbij wordt voortgebouwd op de intuïtieve ervaringen van leerlingen met balans (variërend van leren lopen tot het spelen op een wip) en kennis die ze al hebben, lijkt dus een kansrijke aanpak voor het ontwikkelen van de HOV van basisschoolleerlingen.

 

De ontwikkeling van het algebraïsch redeneren gedurende de lessen

In Deelstudie 2 (Otten, Van den Heuvel-Panhuizen, Veldhuis & Heinze, 2019) onderzochten we de ontwikkeling van het algebraïsch redeneren van 65 leerlingen uit groep 7 gedurende de zes lessen van de lessenserie (afbeelding 3). Deze leerlingen hadden geen eerdere lessen gehad over het oplossen van vergelijkingen. Gedurende de lessen redeneerden de leerlingen over lineaire vergelijkingen in verschillende contexten (afbeelding 3). De rol van de leerkracht bestond voornamelijk uit doorvragen op hun redeneren en vragen te stellen als ‘Hoe weet je dit?’ en ‘Kan je dat uitleggen?’ Ook werden verschillende manieren besproken om de problemen om te lossen, waarbij de input van de leerlingen altijd leidend was. Tijdens de lessen vond een duidelijke ontwikkeling plaats in het redeneren van de leerlingen over deze vergelijkingen. We zoomen in op Julia (10 jaar) om deze ontwikkeling te illustreren. Tijdens het werken met de hangmobiel in de eerste les (zie afbeelding 2 voor de exacte samenstelling van de hangmobiel), redeneert ze samen met Kees (afbeelding 4) over de vraag of ze iets kunnen veranderen aan de hangmobiel, terwijl ze zeker weten dat deze recht zal blijven.

 

Kees: Oja deze twee [wijst naar de twee rode balletjes aan de linkerkant] zijn al deze [wijst naar de twee rode balletjes aan de rechterkant].

Julia: Dan moeten deze twee zwarte [wijst naar twee zwarte balletjes aan de rechterkant] wel even zwaar zijn als 1, 2, 3, 4, 5, 6 [wijst één voor één de witte balletjes aan de linkerkant aan]

Kees: Ja!

Julia: Dan zijn dat [wijst naar een zwart balletje] dus drie witte

Kees: Ja dus dan kunnen we dit [zwarte balletje] ruilen en daar drie [witte balletjes] voor geven.

 

In deze dialoog komt duidelijk naar voren dat Julia en Kees tijdens het in balans houden van de hangmobiel op een intuïtieve manier informele algebraïsche strategieën toepassen en ontwikkelen. Hun idee dat dezelfde balletjes aan beide kanten van de hangmobiel (oftewel: gelijke onbekenden aan beide kanten van de vergelijking) elkaar in evenwicht houden en elkaar dus opheffen, duidt op begrip van de isolatiestrategie. Het idee dat balletjes in de juiste verhouding elkaar kunnen vervangen duidt op begrip van de substitutiestrategie. Na afloop van deze dialoog voerden Julia en Kees de besproken handeling uit. Ze wisselden één zwart balletje van de rechterkant met drie witte balletjes aan de linkerkant (oftewel: ze herstructureerden de hangmobiel) en zagen de hangmobiel opnieuw in balans komen.

 

In deze deelstudie vonden we verschillende aanwijzingen voor een relatie tussen de ervaringen van leerlingen met het fysieke balansmodel en hun gebruik van strategieën en notaties om problemen op te lossen in andere contexten. Zo maakten leerlingen gebruik van de strategieën die ze ontwikkeld hadden tijdens het werken met de hangmobiel, of sommige leerlingen gebruikten een representatie van het model voor het oplossen van een stelsel van twee symbolische vergelijkingen. Een mooi voorbeeld hiervan is de oplossing van Julia van een probleem aan het einde van les 6 (afbeelding 5). In haar oplossing zet ze de vergelijkingen eerst om in hangmobielen. Ze isoleert onbekende M, waarbij ze gebruikt maakt van de tweede vergelijking. Vervolgens substitueert ze in de eerste vergelijking de M voor LL, waardoor ze de waarde van L kan berekenen. Tenslotte substitueert ze die waarde van L in de eerste vergelijking, om zo de waarde van M te vinden. Julia kiest er in dit voorbeeld overigens voor om 2L te noteren als LL. In les 4 werd aandacht besteed aan het noteren van onbekenden. Zo werd bij het redeneren over informele vergelijkingen in de touwtrek-context (afbeelding 3, les 4) besproken dat je de kracht van de drie schapen kan weergeven door een tekening, maar dat je ook voor andere manieren van noteren kon kiezen. Leerlingen kwamen toen zelf met alternatieve ideeën, zoals een weergave met letters (vb. SSS, 3S) of met andere symbolen (vb. ooo). Julia koos toen voor S + S + S.

 

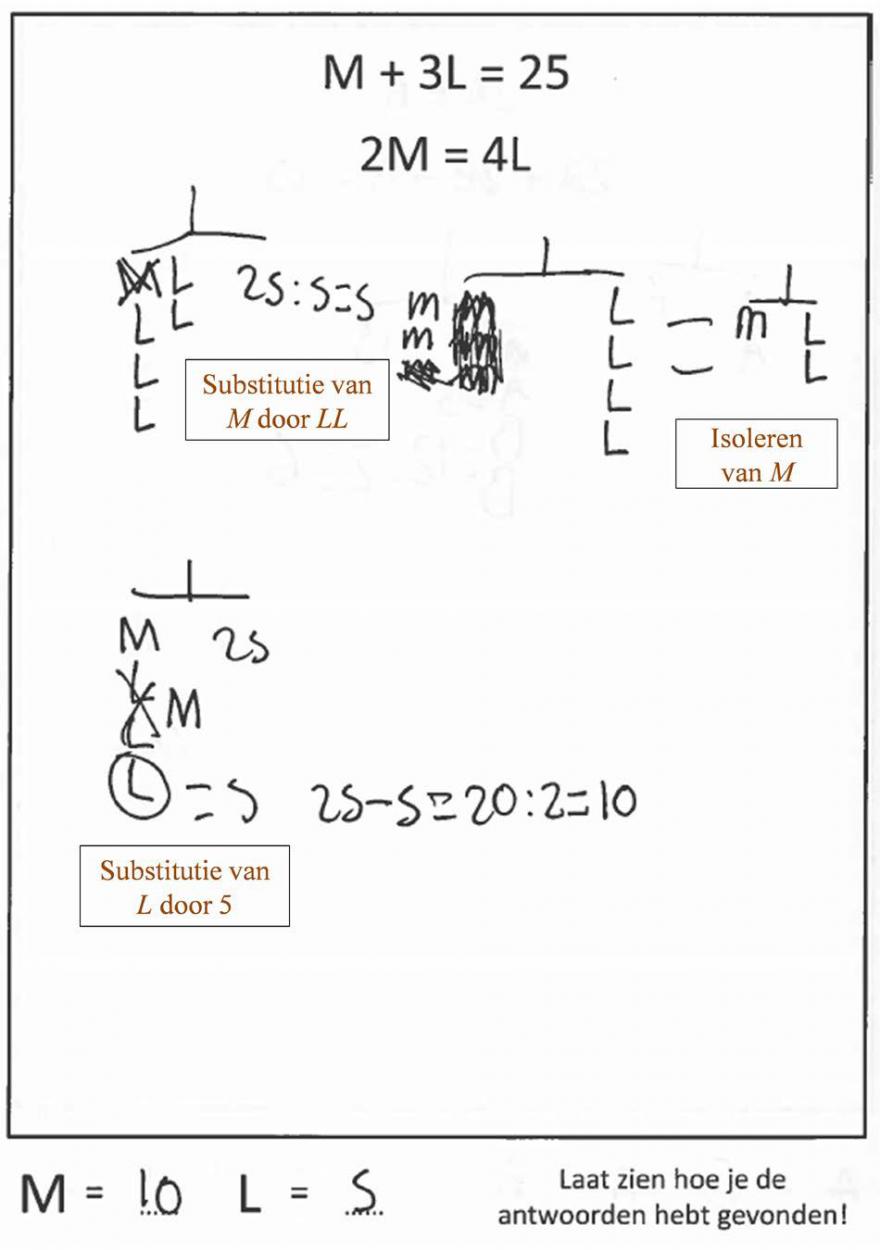
Uit de analyse van het redeneren van alle leerlingen bleek dat leerlingen duidelijk vooruitgingen gedurende de lessen. Na het volgen van de lessen kon bijvoorbeeld 77% van de leerlingen de waarden vinden van onbekenden M en L in het bovengenoemde stelsel van vergelijkingen (afbeelding 5). Leerlingen gingen vooruit in het combineren van de informatie van beide vergelijkingen en ze werden beter in het uitleggen van hun redeneren en in het opschrijven van de gebruikte algebraïsche strategieën.

 

De rol van fysieke ervaringen

De leeromgeving met het fysieke balansmodel bleek dus een goede context voor het ontwikkelen van algebraïsch redeneren. In Deelstudie 3 (Otten, Van den Heuvel-Panhuizen, Veldhuis, Boom & Heinze, 2020) voerden we een quasi-experimentele studie uit waarin we zowel de effecten van onze lessenserie (afbeelding 3) op de langere termijn, als de specifieke bijdrage van fysieke ervaringen met het balansmodel onderzochten. Aan dit onderzoek namen 212 leerlingen uit groep 7 deel, die geen eerdere lessen hadden gehad over vergelijkingen. De leerlingen werden verdeeld over twee interventiecondities en een controleconditie. Drie klassen kregen de eerder beschreven lessenserie maar dan met een representatie van het balansmodel op papier (rechts in afbeelding 2) in plaats van een fysiek model, drie klassen kregen exact dezelfde zes lessen maar dan met de toevoeging van een fysiek balansmodel (links in afbeelding 2 en Deelstudie 2), en drie klassen in de controleconditie kregen les over een ander wiskundig onderwerp, namelijk over kans. Hierdoor konden we de toegevoegde waarde van de fysieke ervaringen met een concreet model onderzoeken. In deze studie gebruikten we een zogenoemd staged-comparison design. Dit hield in dat het redeneren van leerlingen over stelsels van twee informele lineaire vergelijkingen op vier momenten gedurende het schooljaar schriftelijk gemeten werd (zie afbeelding 2 voor één van de taken). Tussen twee van deze meetmomenten kregen leerlingen de lessen, waardoor we het effect van de lessen op het algebraïsch redeneren van de leerlingen zowel kwalitatief als kwantitatief konden onderzoeken.

 

Deelname aan de lessen leidde tot een hoger niveau van redeneren over (d = 0.73; dit betekent een middelmatig tot groot effect). De leerlingen werden beter in het combineren van de informatie van beide vergelijkingen in hun redeneren: dit hoogste niveau van redeneren kwam meer voor na afloop van de interventie (65%) dan ervoor (39%). Neem als voorbeeld het probleem uit afbeelding 1. Een redenering bij dit probleem wat in deze hoogste categorie viel, was ‘27-10-10=7, dus het sokje = 7. Dan moet het speentje 3 zijn, want 3+7=10’. De leerling isoleert hier het sokje door de tweede vergelijking tweemaal van de eerste vergelijking af te trekken (eliminatie strategie), en combineert dus de informatie van beide vergelijkingen. Het kwam tegelijkertijd juist minder voor dat leerlingen lagere niveaus van redeneren lieten zien waarbij ze geen enkele van de vergelijkingen gebruikten (antwoorden als ‘ik heb gegokt’ of ‘dat zie ik gewoon’) of maar één van beide vergelijkingen (antwoorden als ‘het speentje is 5, want dat is de helft van 10’). Hoewel leerlingen die les hadden gehad met zowel een fysiek balansmodel als een representatie van het model op papier een grotere vooruitgang in het hoogste niveau van redeneren (een toename van 33%) lieten zien dan leerlingen die alleen les hadden gehad met een representatie van het model op papier (toename van 18%), was dit verschil niet significant (p = .136). Inzoomen op het redeneren van de leerlingen liet daarentegen wel zien dat de leerlingen die ook met het fysieke model hadden gewerkt vaker een representatie van het model gebruiken in hun redeneren (17% vs. 1%) en vaker gebruik maakten van geavanceerde algebraïsche strategieën zoals substitutie of eliminatie (60% vs. 40%).

 

Effect op een ander wiskundig domein

In de vorige twee deelstudies toonden we het effect aan van onze lessenserie op het redeneren over stelsels van vergelijkingen. Het redeneren over en het oplossen van dergelijke stelsels van vergelijkingen vraagt om wiskundige HOV, zoals het vermogen van de leerlingen om te redeneren over covariantie (Thompson & Carlson, 2017), oftewel, redeneren over de samenhang tussen bepaalde variabelen. Neem als voorbeeld wederom het probleem in afbeelding 1: hier moeten leerlingen redeneren over de samenhang tussen de waarde van het sokje en de waarde van het speentje. Dit redeneren over covariantie is ook relevant binnen andere wiskundige domeinen, zoals grafieken van beweging (Leinhardt et al., 1990). Het begrijpen van een afstand-tijd grafiek vereist bijvoorbeeld dat leerlingen de samenhang doorzien tussen de variabelen afstand en tijd, en dat ze doorzien dat veranderingen in de één samengaan met veranderingen in de ander. De overeenkomst tussen de domeinen van vergelijkingen en grafieken riep de vraag op of het stimuleren van het redeneren over vergelijkingen mogelijk ook leidt tot een verbetering in het redeneren over grafieken. Onze laatste deelstudie, Deelstudie 4 (Otten, Duijzer, Van den Heuvel-Panhuizen, Veldhuis, Boom, Doorman & Leseman, 2020), betrof een exploratieve studie naar het effect van onze lessenserie op het redeneren over grafieken. Uit deze studie bleek dat deelname aan de algebralessen leidde tot een verbetering in het algebraïsch redeneren van deze leerlingen, maar niet tot een verbetering van het grafisch redeneren. Op basis hiervan kunnen we voorzichtig de conclusie trekken dat het ontwikkelen van HOV gedurende de lessen over vergelijkingen niet resulteerde in het ontwikkelen van HOV binnen het domein van grafieken. De overdracht van HOV van het ene wiskundige domein naar een (gerelateerd) ander wiskundig domein lijkt dus niet vanzelfsprekend.

 

Conclusies en aanbevelingen voor de praktijk

Dit promotieonderzoek laat duidelijk zien dat het mogelijk is om het algebraïsch redeneren van leerlingen op de basisschool te stimuleren. Door al op de basisschool te starten met het aanbieden van activiteiten die het (informeel) algebraïsch redeneren van leerlingen bevorderen, kan een doorlopende leerlijn gecreëerd worden van de basisschool tot en met de middelbare school. Het belang van zulke doorlopende leerlijnen in het reken-wiskundeonderwijs wordt steeds meer onderschreven op zowel nationaal (curriculum.nu, 2019) als internationaal niveau (National Council of Teachers of Mathematics [NCTM], 2000). Daarnaast kan het stimuleren van algebraïsch redeneren gezien worden als een manier om wiskundige HOV binnen het basisonderwijs te bevorderen en zo het reken-wiskundecurriculum op de basisschool te verrijken. We komen dan ook met de sterke aanbeveling om algebra (meer) op te nemen in het reken-wiskundecurriculum van de basisschool.

 

Het opnemen van algebra in het basisonderwijs brengt echter wel bepaalde uitdagingen met zich mee. Of, om in de woorden van de titel van mijn proefschrift te spreken: op een aantal punten is het nog wel zoeken naar balans. De eerste uitdaging is om nog meer zicht te krijgen op hoe het algebraïsch redeneren van basisschoolleerlingen het best gestimuleerd kan worden. Voor het stimuleren van redeneren over vergelijkingen blijken activiteiten met een balansmodel waarmee leerlingen redeneren over relaties tussen onbekenden waardevol te zijn. Hierdoor ontwikkelden leerlingen in ons onderzoek verschillende algebraïsche strategieën, die ze in een later stadium konden gebruiken voor het oplossen van (stelsels van) vergelijkingen in nieuwe contexten en zelfs voor het oplossen van stelsels van formele vergelijkingen. Daarentegen kunnen we op basis van ons onderzoek geen eenduidige conclusies trekken over de toegevoegde waarde van de fysieke ervaringen met een concreet balansmodel, omdat we geen significant verschil vonden tussen de condities in Deelstudie 3. Dit moet dan ook verder onderzocht worden. De tweede uitdaging is dat het huidige (reken-wiskunde)curriculum op de basisschool al overvol is. We moeten ervoor waken dat het opnemen van algebra in dit curriculum er niet toe leidt dat het curriculum alleen maar voller wordt. Algebra moet dus niet simpelweg toegevoegd worden aan het curriculum; het moet geïntegreerd worden. Door kleine aanpassingen door te voeren in de activiteiten die momenteel al plaatsvinden, kunnen deze worden ingezet om het algebraïsch redeneren van leerlingen te stimuleren. Dit kan al beginnen bij jongste leerlingen. Hier kan je bijvoorbeeld denken aan allerlei activiteiten met fysieke balansweegschalen – die momenteel vaak vanaf de kleuters al gebruikt worden voor verschillende activiteiten zoals koken – waarmee leerlingen vanaf jongs af aan ervaringen op kunnen doen met het herkennen, het creëren en het behouden van gelijkheid. Vervolgens kan dit met de jaren uitgebreid worden naar het oplossen van vergelijkingen in allerlei informele contexten en uiteindelijk naar het oplossen van formele vergelijkingen. De derde uitdaging is het ondersteunen van basisschoolleerkrachten op het onderwijzen van algebra. Hierbij is het belangrijk dat leerkrachten meer inzicht krijgen in de aard van dergelijke activiteiten, in het belang van het integreren van dit soort activiteiten in het basisonderwijs en in het vermogen van basisschoolleerlingen om algebraïsch te redeneren. Dit vereist integratie van dit onderwerp in de lerarenopleiding, het zou bijvoorbeeld mooi passen bij modules rondom verhoudingen of getalbegrip, en het vraagt om nascholingsactiviteiten. De laatste uitdaging is om ervoor te zorgen dat alle leerlingen deel kunnen nemen aan activiteiten die het algebraïsch redeneren stimuleren, en niet alleen een select groepje best-presterende leerlingen zoals nu vaak het geval is bij dit soort activiteiten (bijvoorbeeld bepaalde opdrachten in Rekentijgers). Een manier om dit te verwezenlijken, is door (alle) leerlingen al op jonge leeftijd te laten participeren in activiteiten die voortbouwen op hun intuïtieve ervaringen met balans, en door dit als basis te nemen voor het stimuleren van hun algebraïsch redeneren over vergelijkingen.