Het mooie wiskundige bouwwerk als springplank voor de leraar
UCLL, Art of Teaching
Het mooie wiskundige bouwwerk was het vertrekpunt voor ons praktijkonderzoek van de laatste twee jaar. Door observaties in klassen en gesprekken met leraren en lerarenteams, ontdekten we hoe leerlingen slechts beperkte cognitieve schema’s voor wiskunde ontwikkelen. We brachten mogelijke oorzaken in kaart.
Vanuit die analyse formuleerden we de hypothese: ‘als leraren goed zicht hebben op leerlijnen, een coherent jaarplan maken en de leerstof aanbieden in grotere betekenisvolle gehelen, krijgen ze meer slagkracht om bij leerlingen rijke schema’s te ontwikkelen’. We gebruikten de wiskundige opbouw van leerinhouden als basis om materialen te ontwikkelen waarmee leraren hun praktijk kunnen onderzoeken en anders vormgeven.
Die denkwijze en deze materialen hebben we zelf een jaar lang in het zesde leerjaar/groep 8 uitgetest. Daarnaast legden we deze materialen bij studenten in de lerarenopleiding en in gesprekken met leraren(teams). Dat bracht rijke discussies op gang die ervoor zorgden dat leraren andere keuzes durfden maken en zo hun wiskundeonderwijs versterkten.
Inleiding
Als lerarenopleiders wiskunde voor het basisonderwijs zijn wij, Michèle Dexters en Els Van Emelen, voortdurend op zoek naar hoe we onze passie voor het prachtige wiskundige bouwwerk kunnen doorgeven aan de volgende generatie. Daarvoor verdiepen we ons graag in wat er in het onderwijs aan de hand is. De uitspraak ‘de leraar opnieuw aan het roer’ (Brinckman & Versluys, 2021; De Man, 2022) houdt al enige tijd onze aandacht vast. Dat dit niet vanzelfsprekend is, wordt duidelijk in het praktijkonderzoek dat we de laatste twee jaar voerden.
Omdat we beiden in Vlaanderen werken, is dat ook de plek waar het onderzoek plaatsvindt. De Vlaamse context is niet helemaal dezelfde als de Nederlandse. Zo wordt bijvoorbeeld het basisonderwijs in Vlaanderen opgesplitst in drie jaar kleuteronderwijs en zes jaar lagere school. Groep 3 in Nederland komt overeen met het eerste leerjaar in Vlaanderen, groep 8 met het zesde leerjaar. Ook de terminologie verschilt af en toe: het woord ‘sommen’ wordt in Vlaanderen alleen voor ‘optellingen’ gebruikt, bij een verschil wordt over een ‘aftrekking’ gesproken. Toch ondervinden Nederlandse kinderen vaak dezelfde hindernissen als Vlaamse wanneer ze wiskunde leren.
Dit artikel bestaat uit drie grote delen. In het eerste deel vertrekken we van een aantal observaties in basisscholen. We merken op dat leerlingen vaak losse flodders leren en dat dit tot arme cognitieve schema’s leidt. We gaan op zoek naar mogelijke oorzaken en oplossingen.
In deel twee lees je meer over ideeën en middelen die we ontwierpen om leraren, teams en studenten te helpen om rijke cognitieve schema’s te ontwikkelen. We vertrekken hiervoor van de hypothese: ‘als leraren goed zicht hebben op leerlijnen, een coherent jaarplan maken en de leerstof aanbieden in grotere betekenisvolle gehelen, krijgen ze meer slagkracht om bij leerlingen rijke cognitieve schema’s te ontwikkelen’. We geven een beeld van hoe leerlijnen, jaarplannen en leerbogen vorm kunnen krijgen. Dit illustreren we met voorbeelden over rationale getallen[1].
In het derde deel beschrijven we hoe we in de praktijk met leerlijnen en leerbogen aan de slag gaan en wat dat ons leert. Zo gebruiken teams van leraren de aangeboden leerlijnen om discussie over hun wiskundeonderwijs op gang te brengen en het te versterken. Daarnaast leiden we studenten op om zelf leerbogen te ontwikkelen. En tenslotte hebben we de aanpak ‘leerlijn – jaarplan – leerboog’ zelf een jaar lang in het zesde leerjaar uitgetest. Ook daarover brengen we kort verslag uit.
Het wiskundeonderwijs onder de loep
Losse flodders leren
Bij de start van het onderzoek verzamelen we materiaal vanuit verschillende bronnen. We observeren wiskundelessen in verschillende leerjaren van het basisonderwijs, voeren hierover gesprekken met leraren en nemen deel aan overleg tussen leraren. Daarnaast verdiepen we ons in het materiaal van verschillende wiskundemethodes en de bijbehorende werkboeken voor leerlingen.
Naarmate onze observaties en gesprekken vorderen, krijgen we hoe langer hoe meer de indruk dat leerlingen tijdens de wiskundelessen vaak losse flodders leren. Dat maakt het moeilijk om met nieuwe leerstof verder te bouwen op voorgaande kennis. Terwijl dat voorbouwen bij wiskunde essentieel is. Nieuwe inzichten steunen immers bijna altijd op eerder verworven inzichten. Afbeeldingen 1, 2 en 3 tonen enkele van deze observaties.
Observatie 1. Splitsen en verdelen
De waarde van expliciteren: splitsen en verdelen
In het zesde leerjaar/groep 8 leren kinderen strategieën om handig te rekenen. Tijdens een observatie zien we meester Kristof de volgende strategie om te delen aanleren:
2673 : 9 = (2700 – 27) : 9
= (2700 : 9) – (27 : 9)
= 300 – 3
= 297.
De eigenschap waarop deze strategie steunt, namelijk de deling is linksdistributief ten opzichte van de optelling/aftrekking, noemen we in het basisonderwijs ‘splitsen en verdelen’. We splitsen het deeltal in een verschil dat we ‘verdelen’ over de deler.
Tijdens de les vinden de leerlingen het niet gemakkelijk om te begrijpen dat deze werkwijze ook een goed antwoord oplevert. Nochtans is deze strategie een variant van een eigenschap die ze vroeger al voor andere opgaven gebruikten. Alleen wordt hierboven het deeltal in een verschil gesplitst, terwijl dat vroeger een som was. Het lijkt alsof leerlingen geen verband tussen beide zien.
2745 : 9 = (2700 + 45) : 9
= (2700 : 9) + (45 : 9)
= 300 + 5
= 305.
Ter verduidelijking noteert de leraar deze tweede oefening op het bord. Ella, een meisje dat wiskunde gewoonlijk snel doorziet, steekt aarzelend haar vinger op en zegt dat ze het vanaf de tweede stap, (2700 + 45) : 9, niet meer begrijpt. Als de leraar verwijst naar het ‘splitsen en verdelen’, lijkt het alsof de leerlingen nog nooit van deze eigenschap hebben gehoord.
Interpretatie
Wanneer we dit soort oefeningen in de werkboeken van de leerlingen opzoeken, zien we dat ze dit soort oefeningen als volgt oplossen:
2745 : 9 = 305
/ \
2700 45
↓ ↓
300 5
We merken dat de leerlingen wel techniekjes beheersen om deze opgaven op te lossen, maar dat ze niet geoefend zijn in de achterliggende correcte wiskundige notaties. Dat zorgt ervoor dat de eigenschappen niet zichtbaar zijn én dus ook niet worden geëxpliciteerd. Dit start al veel vroeger. In het derde leerjaar/groep 5 leren kinderen vermenigvuldigingen zoals 24 x 8 uitrekenen:
24 x 8 = (20 + 4) x 8 = (20 x 8) + (4 x 8) = 160 + 32 = 192
Je kan de eigenschap van het ‘splitsen en verdelen’ hier eenvoudig met materiaal visualiseren. Echter, zonder dat je je er als leraar bewust van bent, verschuift de focus al snel van het ‘aantonen van een eigenschap’ naar het ‘vinden van een techniek om deze opgaven op te lossen’. Het wordt dan een losse regel. Als leerlingen de tweede en derde stap nooit hoeven te noteren, versterk je dit nog. Dat is erg jammer, niet alleen omdat de bovenstaande strategie van handig rekenen hierop steunt, maar ook omdat deze manier van denken de basis vormt om in het secundair/voortgezet onderwijs met letters te rekenen:
![]()
Observatie 2. De oppervlakte van vlakke figuren
De kracht van formules ontdekken: de oppervlakte van vlakke figuren
Juf Roos is leraar in het zesde leerjaar/groep 8. Ze tekent een trapezium op het bord en vraagt de leerlingen hoe ze de oppervlakte van deze figuur kunnen berekenen. Een leerling stelt voor om twee verticale lijnstukken te tekenen zodat er een rechthoek en twee driehoeken ontstaan. De leerlingen meten de basissen en de hoogtes van deze figuren en berekenen de oppervlaktes van de twee driehoeken en de rechthoek. Daarna tellen ze de drie oppervlaktes op.
Interpretatie
De laatste decennia werd de hoeveelheid parate kennis in het basisonderwijs in Vlaanderen sterk verminderd. Zo leren de leerlingen enkel nog de formule voor de oppervlakte van een rechthoek, een parallellogram en een driehoek. Om de oppervlakte van andere figuren te vinden, gebruiken ze het omstructureren als techniek. Omstructureren is het opdelen van de figuur in stukken, die je eventueel verplaatst, zodat je de figuur herleidt tot figuren waarvan je de oppervlakte wel kan berekenen. Voordien gebruikten we deze techniek om de oppervlakteformules voor de verschillende vlakke figuren af te leiden. Voor een trapezium ziet dat er als volgt uit:
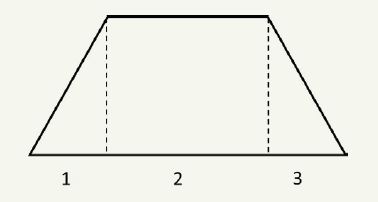
We delen het trapezium op in twee driehoeken. (Hetzelfde trapezium omgekeerd naast de eerste plaatsen, levert gelukkig dezelfde formule op.)
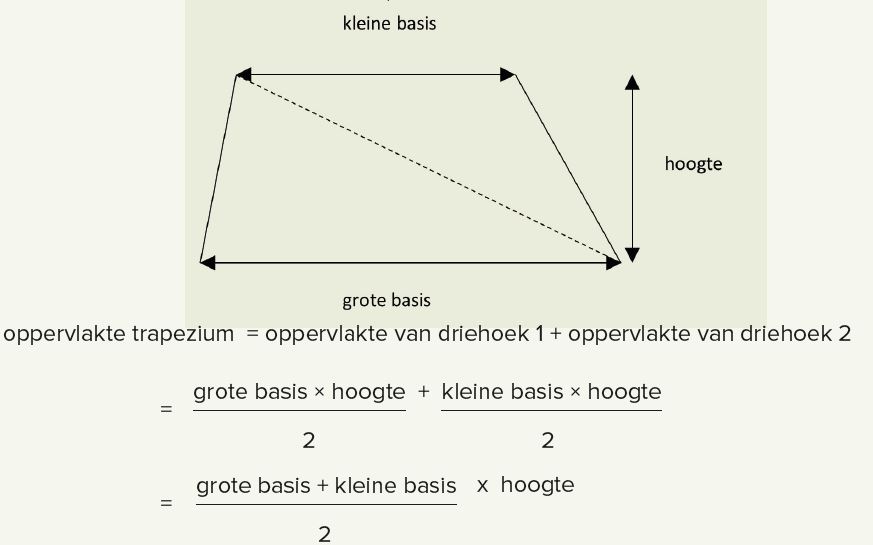
Als we de werkboeken onderzoeken, merken we dat leerlingen veel tijd spenderen aan het opdelen van figuren tot rechthoeken en driehoeken en vooral rekenwerk verrichten. Het leren omstructureren wordt een doel op zich en vormt niet langer een onderdeel van een groter geheel.
De kracht van een formule blijft onderbelicht. In dit voorbeeld: deze formule is geldig voor alle soorten trapezia en vermindert het (reken)werk. Ook hoe je een formule correct gebruikt, krijgen leerlingen te weinig mee. Bijvoorbeeld: wat is de hoogte in deze driehoeken? Bovendien is er te weinig aandacht voor de voorwaarden waaronder je een formule kan afleiden. Je mag immers niet redeneren vanuit een speciale figuur om een algemeen geldende formule af te leiden. Dit legt krediet op de ontwikkeling van wiskundige feeling bij kinderen.
Observatie 3. Introductie van kommagetallen
Probleemstellingen aanbieden vanuit wiskunde: introductie van kommagetallen
In het derde en vierde leerjaar/groep 5 en 6 komen leerlingen in contact met breuken en daarnaast, maar los daarvan, met kommagetallen. Beide concepten worden vanuit de leefwereld van de kinderen geïntroduceerd. Kommagetallen brengen we vaak vanuit geld of meetervaringen aan, terwijl pizza’s of taarten voor breuken een herkenbare context zijn. Voor de leerlingen lijkt het of beide onderwerpen weinig of niets met elkaar te maken hebben. Pas in het vijfde leerjaar/groep 7 komt het verband tussen kommagetallen en breuken aan bod. In praktijk komt het er vaak op neer dat leerlingen lijstjes van gelijkwaardige kommagetallen, breuken en percentages uit het hoofd leren.
Interpretatie
Wanneer je echter vanuit het bouwwerk van wiskunde denkt, is het erg mooi om het concept van breuken als vertrekpunt te gebruiken en de kommagetallen hieruit te laten voortvloeien. Concreet kan dat er als volgt uitzien:
De introductie van breuken start met het nemen van een breuk van een geheel (¾ van een taart). Later passen we deze denkwijze toe op aantallen (¾ van 24). In het vierde leerjaar/groep 6 zetten we een volgende stap en maken we de afspraak dat onbenoemde breuken, bijvoorbeeld ¾, breuken zijn die we van de eenheid nemen. Dit concept noemen we breuk als rationaal getal. Visueel helpt het om breuken op de getallenas te plaatsen.

De genoteerde breuken verschillen erg van de natuurlijke getallen (0, 1, 2, … 10, 11 , 12 …, 100, … , 1000…). We maken voor een breuk immers gebruik van twee getallen, een teller en een noemer. Je kan leerlingen de vraag stellen of de notatie van breuken ook op een andere manier kan, op een manier die dichter bij de gekende natuurlijke getallen ligt. Wanneer je op dat moment kommagetallen aanbiedt, krijg je daarop een mooi antwoord en werk je meteen aan de volledige ontwikkeling van het begrip ‘rationaal getal’.
Arme of onvolledige cognitieve schema’s
We verdiepen ons in literatuur. In het eerste hoofdstuk van het boek ‘Handboek wiskundedidactiek’ (Drijvers, Van Streun, & Zwaneveld, 2019) legt Paul Drijvers een interessant concept op tafel dat helder maakt wat het probleem is. Hij verwoordt:
‘De kennis in het langetermijngeheugen organiseren we in cognitieve schema’s. Dat zijn mentale structuren, die we ons kunnen voorstellen als netwerken van knooppunten (feiten, concepten, procedures, beelden) die onderling verbonden zijn door relaties ertussen (… hangt samen met …, … geeft een beeld van …, … is een alternatieve aanpak voor …, enzovoort).
_w880.jpg)
Rijke, betekenisvolle en zo compleet mogelijke cognitieve schema’s (afbeelding 4, links) maken het mogelijk om op een flexibele, wendbare manier problemen aan te pakken. Experten in een vakgebied bezitten samenhangende schema’s die hen in staat stellen om doelgerichter problemen aan te pakken. Wanneer je cognitieve schema’s echter gefragmenteerd zijn, kan je veel minder aanknopingspunten vinden om ze op te lossen.’ (Drijvers, Van Streun, & Zwaneveld, 2019, pp. 28-29)
Drijvers vermeldt vervolgens dat:
‘… het opsplitsen van leerstof in hapklare brokken wel succes heeft op korte termijn, maar leidt tot het opslaan in het geheugen van kleine, onsamenhangende schema’s (afbeelding 4, rechts). Deze verbrokkeling heeft mede tot gevolg dat leerlingen dénken dat ze iets begrijpen, terwijl het schema onvolledig is.’ (ibid, pp. 28-29)
We herkennen deze vaststellingen in onze observaties. Leerlingen leren vaak losse entiteiten die ze op het einde van de les kunnen inzetten, maar die niet of maar weinig in een globale structuur ingebed zijn. De observaties in afbeeldingen 1, 2 en 3 zijn hier voorbeelden van.
In de lerarenopleiding geven we toekomstige leraren mee dat het leren van wiskunde in de basisschool een dubbele finaliteit heeft. Enerzijds leren kinderen inhouden die een directe impact hebben op het goed functioneren in de maatschappij, zoals bijvoorbeeld het uitrekenen van een vermenigvuldiging, het berekenen van de oppervlakte van een kamer of de hoeveelheden voor de benodigdheden van een recept.
Daarnaast heeft het wiskundeonderwijs in de basisschool echter een tweede taak. We willen bij kinderen wiskundige feeling ontwikkelen en hen inhouden bijbrengen die als basis dienen voor hun verdere studieloopbaan. Zo bereidt het leren kennen van eigenschappen als ‘van plaats wisselen’ en ‘splitsen en verdelen’ voor op rekenen met letters bij algebra. Een ander voorbeeld is het veralgemenen van voorbeelden als eerste stap naar bewijzen. En het vaardig leren tekenen van meetkundige figuren is een aanzet tot het construeren op basis van meetkundige eigenschappen. Op die manier leggen we kiemen voor goede samenhangende cognitieve schema’s. Tijdens onze observaties ervaren we dat die tweede functionaliteit in basisscholen ondergesneeuwd raakte.
Rijke en volledige cognitieve schema’s opbouwen
Bij leerlingen samenhangende cognitieve schema’s ontwikkelen, is geen sinecure. Het is een langdurig proces waarvoor een duidelijke doorgaande lijn doorheen de basisschool en voldoende vakexpertise bij de leraar nodig is. Voor dit onderzoek brengen we – zonder volledigheid na te streven – een aantal elementen in kaart die dit proces kunnen ondersteunen.
Expertise helpt
Wanneer je als leraar zelf over degelijke vakkennis, die samenhangend en goed georganiseerd is, beschikt, kan je dit gemakkelijker bij je leerlingen ontwikkelen. Dat betekent immers dat je zicht hebt op de leerinhouden die leerlingen verwerven én weet waar die naartoe zullen leiden of waarop ze voorbereiden. Deze kennis helpt je om beslissingen te nemen over welke leerstof je aanbiedt en op welke manier je dat doet.
De laatste decennia is de instroom van studenten aan de lerarenopleiding verschoven van hoofdzakelijk ASO-studenten (vergelijkbaar met vwo in Nederland) naar studenten uit eerder technische richtingen (vergelijkbaar met mbo in Nederland) met meestal een beperkte hoeveelheid wiskunde. Studenten die komen uit een richting met een groot pakket wiskunde, zijn eerder uitzonderingen in deze opleiding. Nochtans is wiskunde geven – ook aan jongere kinderen – bijzonder boeiend. Dit zichtbaar maken als een waardevol aspect in de taak van leraar, kan jongeren die door wiskunde geboeid zijn, opnieuw stimuleren om leraar te worden.
In combinatie met deze andere instroom, heeft het aandeel wiskunde in de lerarenopleiding plaats moeten maken voor andere opleidingsonderdelen. Leraren basisonderwijs voelen zich vaak geen vakleraar maar eerder een leercoach die leerlingen begeleidt. Wanneer je als (toekomstige) leraar je eigen cognitieve schema’s (verder) wil ontwikkelen vraagt dat inspanning. Inhoudelijke nascholingen kunnen hierbij een waardevolle ondersteuning zijn.
Eindtermen overstijgen
In 1998 voerde de Vlaamse overheid de eindtermen (vergelijkbaar met de kerndoelen in Nederland) voor het basisonderwijs in (Vlaamse overheid, sd). Waar voordien de onderwijsverstrekkers zelf beslissingen konden nemen over de leerstof, bepalen nu de eindtermen grotendeels wat er op het programma staat. Van leerlingen wordt verwacht dat ze op populatieniveau deze doelen bereiken. Om dit na te gaan neemt de overheid toetsen[2] af. Dit laatste is niet zonder gevolgen voor wat er in de klas gebeurt. Het systematisch toetsen op grote schaal beïnvloedt het onderwijs op onverwachte manieren. Deze gedachte leggen we uit aan de hand van twee voorbeelden.
Doelen worden inhouden
In de eindtermen vind je het doel dat leerlingen ‘getallen moeten begrijpen als een hoeveelheid, een rangorde, een verhouding of een code’ (Vlaamse overheid, sd). Als leraar interpreteer je dit als ‘leerlingen moeten ervaringen opdoen met verschillende aspecten van een getal en begrijpen dat een getal voor verschillende dingen worden gebruikt’. Wanneer je dit soort doelen grootschalig wil toetsen, leidt dat al snel tot een meerkeuzevraag waar leerlingen aanduiden welk getalaspect in een opgave aan bod komt.
Dit heeft effect op hoe onderwijs wordt opgezet. Sinds enige tijd bevatten handboeken rijtjes opgaven waar leerlingen het getalaspect moeten aanvinken (afbeelding 5). Het doel ‘functies van getallen herkennen en verwoorden’ evolueert op deze manier naar een inhoud, ‘het classificeren van verschillende contexten in verband met getallen’. En classificeren is veel gezegd. Aanvinken is een betere beschrijving.

Streven naar minimumdoelen leidt tot niveauverlaging
Daarnaast heeft het invoeren van de eindtermen en het grootschalig toetsen ervan nog een ander effect. Eindtermen zijn minimumdoelen en de leerstofinhoud is dus bewust beperkt gehouden. Het woordje minimum wordt in praktijk echter grotendeels genegeerd. Sterker nog, het invoeren van deze doelen heeft ervoor gezorgd dat scholen, handboeken en leraren zich richten op het bereiken ervan, maar niet langer streven naar een hoger niveau. Daardoor komt de lat een stuk lager te liggen. Het inrichten van landelijke toetsen zal deze beweging mogelijk nog verder versterken.
Aangezien de eindtermen minimumdoelen zijn, is er echter geen enkele reden waarom we ons zouden laten tegenhouden om meer te ambiëren. Integendeel, bezig zijn met de leerstof boven de lat, helpt mee om de leerstof onder de lat goed in de vingers te krijgen. Om het met een metafoor te zeggen: ‘als je wilt dat leerlingen vijfentwintig meter zwemmen, jaag je ze niet na vijfentwintig meter uit het zwembad. Nee, als we oefenen op honderd meter zwemmen, zal niet iedereen de honderd meter halen maar wel (bijna) iedereen de vijfentwintig.’ (Van Emelen, 2019).
Twee voorbeelden maken dit concreet:
- In de eindtermen staat enkel de formule voor het volume van een balk. Met relatief weinig extra investering leren leerlingen ook het volume van een (recht) prisma[3] en een cilinder. Dit levert de mooie, algemenere formule op die voor al deze rechte lichamen – en dus ook voor een balk – bruikbaar is:
volume prisma of cilinder = oppervlakte grondvlak x hoogte
Wat een gemiste kans…
- Bewerkingen met breuken wordt in de eindtermen beperkt tot optellen/aftrekken van breuken en een breuk vermenigvuldigen met een getal. Wanneer we echter alle bewerkingen met breuken aanleren, levert dit een zeer mooie vereenvoudiging op van het aantal regels dat we nodig hebben. We kunnen immers terugvallen op drie regels: eentje voor optellen en aftrekken, eentje voor vermenigvuldigen en eentje voor delen. Het is mooi meegenomen dat oefenen op het rekenen met breuken een goede voorbereiding op het abstractere rekenen met letters(Schmeier, 2019). Werken met grotere leerstofgehelen die niet verspreid zijn over basisschool en secundair/voortgezet onderwijs, helpen om een doorgaande lijn op te zetten.
Alhoewel de zin ‘meten is weten’ door beleidsmakers vaak gebruikt wordt om landelijke toetsen te verantwoorden, is het goed om stil te staan bij de onbedoelde effecten van zo een meting. De twee voorgaande voorbeelden illustreren hoe er onbewust mogelijke hindernissen worden ingebouwd die het ontwikkelen van rijke cognitieve schema’s bemoeilijken. Het vraagt van de leraar best wel wat om tegen de stroom in te gaan en de minimumdoelen te overstijgen.
Onderwijzen als kerntaak
Afbeelding 6. Observatie Marie
Ik ga op bezoek bij Marie die stage loopt in het eerste leerjaar (groep 3). Enthousiast begroet Juf Marie de leerlingen als ze de klas binnen lopen. Sommige kinderen geeft ze een high five, anderen komen haar even knuffelen, nog anderen geven haar een deftige handdruk. Tijdens de eerste tien minuten van de les, haalt ze de huiswerkjes op, nemen de kinderen hun rekenboek, hun blokjes en schrijfgerief op de bank, kijken ze naar buiten welk het weer is en mag het kindje van de dag het kalenderblaadje afscheuren.
Als iedereen opnieuw stil zit, zet Marie het bord aan en klikt op het instructiefilmpje. Samen luisteren ze hoe een zachte stem uitlegt hoe je het resultaat kan vinden van negen min twee. Daarna nemen de leerlingen plaats aan de computers aan de zijkant van het klaslokaal en maken oefeningen. Het computerprogramma selecteert automatisch de volgende oefening die de leerling mag maken. Op haar eigen scherm krijgt Juf Marie een overzicht van het aantal juist opgeloste oefeningen per kind. Af en toe steekt een leerling zijn vinger op, gewoonlijk is de computer vastgelopen en start ze die even terug op. Al snel gaat de bel.
De opdracht van een leraar in het basisonderwijs is complex. Als klasleraar is hij verantwoordelijk voor de verschillende vakken die leerlingen krijgen. Daarnaast heeft hij ook een pedagogische verantwoordelijkheid. Bovendien wordt van hem gevraagd op allerlei maatschappelijke problemen in te spelen. Voor dit alles moet hij zich ten aanzien van de overheid, de schoolleiding, de ouders … voortdurend verantwoorden, hetgeen een zware administratieve last met zich meebrengt. Dat alles wordt nog aangevuld met extra-curriculumactiviteiten, zoals sinterklaasfeest, sportklassen of restaurantweekend (afbeelding 6).
Om de werklast haalbaar te houden, zoeken leraren naar oplossingen die hen kunnen ontlasten. Digitale ondersteuning lijkt leraren werk te besparen: filmpjes die instructie geven, het automatisch corrigeren van opdrachten en differentiëren voor verschillende leerlingen. Nochtans zorgt dit ervoor dat leraren veel minder betrokken zijn bij het opzetten en bijsturen van het leren van de kinderen. De ondersteuning leidt hen weg van hun kerntaak: kinderen wiskunde (en andere vakken) leren, daarvoor de geschikte inhouden kiezen en de juiste werkvormen inzetten. Dit betekent niet dat we de computer of het smartbord uit de klas willen bannen, maar wel dat leraren zelf de touwtjes in handen houden en goed nadenken op welke manier deze middelen écht meerwaarde vormen voor het leren. In zijn boek ‘Bordwerk en aantekeningen’ zoekt Marcel Schmeier naar goede combinatie van goed bordwerk en digitale middelen in functie van het leren van kinderen (Schmeier, 2021).
Daarnaast zou het goed zijn om op zoek te gaan hoe we andere taken kunnen vereenvoudigen, afschaffen of ondersteunen. Dat zou een verlichting voor leraren betekenen zodat ze hun kerntaak opnieuw kunnen opnemen, een echte herwaardering van hun job.
Baas boven boek
Om les te geven gaan leraren op zoek naar ondersteuning. Hiervoor val je (gedeeltelijk) terug op rekenmethodes met handleidingen en werkboeken. Wanneer we die onder de loep nemen, valt op hoe lessen hierin zeer gedetailleerd in hapklare activiteiten worden uitgewerkt. Leraren hoeven zich niet in de leerstof te verdiepen maar enkel de opeenvolgende stappen te volgen. Het maakt hen afhankelijk van het aangeboden materiaal, waardoor niet zij, maar de methode de weg bepaalt. Het lijkt hen én leerlingen te begrenzen in plaats van ruimte te geven. Deze methodes zorgen er niet voor dat de leraar aan het roer kan staan, wat nodig is om goede cognitieve schema’s op te bouwen. Ook dit is een illustratie hoe goed bedoelde ondersteuning hen wegleidt van hun kerntaak. De onderstaande voorbeelden illustreren dit idee (afbeelding 7 en 8).
_w880.jpg)
Het principe van herhaling is een waardevol element in het verwerven van leerstof. De vertaling van dit principe, gebeurt hier door de leerstof te verspreiden over aparte lessen over het hele jaar. Stel dat je een leerling bent die de leerstof bijna begrepen heeft. Pas 23 lessen later (blok 5, les 7) komt deze leerstof opnieuw aan bod. De kans is groot dat je tegen dan veel, zo niet alles, vergeten bent van wat je in de eerste les begrepen had.
Door deze fragmentatie is het voor een leraar en leerlingen moeilijk om de opbouw en samenhang van de leerstof te overzien. Dat zorgt ervoor dat leerlingen deze samenhang minder meekrijgen.
Afbeelding 8. Tekst- en denkarm
Tekst-arm en denk-arm (Van Emelen, De kracht van een leerboog, 2020)
De onderstaande opgave past in het zesde leerjaar en is een oefening op stijgingspercentages.
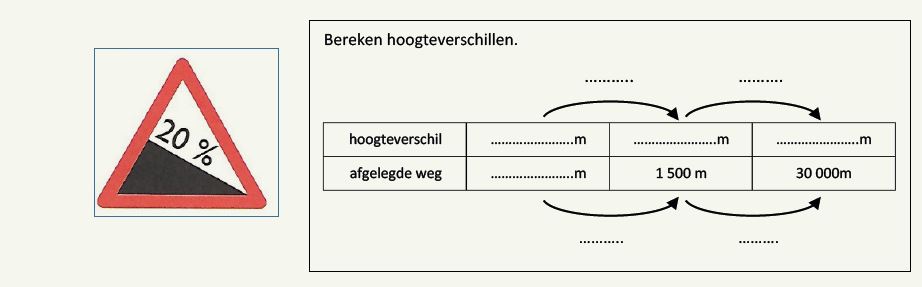
Het valt op hoe weinig woorden in de opgave staan en hoe sterk de oplossing al is voorgestructureerd (Zwik, Tekstarm..., 2019), (Zwik, Tekstrijk, 2020) Je zou kunnen zeggen dat de bovenstaande voorstelling de schematische vertaling is van het vraagstuk:
Op een zonnige dag rijden we door de bergen. We starten een lange beklimming. Langs de kant van de weg staat het bovenstaande verkeersbord. Hoeveel zullen we geklommen zijn nadat we 1 500 m afgelegd hebben? En na 30 000 m?
Door meer context te gebruiken, krijgt de situatie meer betekenis. Enkel tekeningen en tabellen aanbieden, verschraalt de opdracht tot het uitvoeren van berekeningen.
Om voor het bovenstaande vraagstukje tot een oplossing te komen, is veel denkwerk nodig:
1. Welke begrippen spelen mee bij stijgingspercentages? (hoogteverschil en afgelegde weg)
2. Wat betekent een stijgingspercentage van 20%? (100 m afleggen(*) is 20 m stijgen)
3. Zijn dit recht evenredige grootheden? (als de weglengte verdubbelt, verdubbelt ook de stijging. Een verhoudingstabel kan helpen)
4. We hebben geen 100 m afgelegd maar 1 500 m. Hoe berekenen we het hoogteverschil? (15 x afgelegde weg, dus 15 x hoogte)
De tekstarme opgave ontneemt leerlingen de kans om de context waarbinnen deze begrippen gebruikt worden te verkennen. De voorstructurering zorgt ervoor dat leerlingen over verschillende van deze denkstappen niet hoeven na te denken. Het is niet nodig dat ze zich afvragen welke begrippen meespelen, of ze recht evenredig zijn, wat dat betekent, of een tabel kan helpen… De voorstructurering doet dit denkwerk voor hen.
(*) Opmerking: in principe gaat het hier over de horizontale verplaatsing en niet over de afgelegde weg…
Van een wit blad vertrekken en samen met de leerlingen de tabellen opbouwen en hen die laten tekenen, lijkt een tijdrovende bezigheid. Met voorgedrukte tabellen denken we tijd te winnen. We ontnemen leerlingen daarmee echter essentiële denkstappen en denkkansen.
De voorstructurering zorgt er ook voor dat er minder fout loopt doorheen het oplossingsproces. Daardoor lijkt het dat de leerlingen de leerstof beter beheersen. Leren impliceert echter ‘worstelen’ en fouten maken om zicht te krijgen op wat er nodig is voor goede oplossingen. Het is een proces dat traag en moeizaam verloopt en waarvoor het goed is om genoeg tijd te nemen.
De leraar slagkracht geven
Vanuit de bovenstaande analyse zoeken we naar een manier om leraren opnieuw de touwtjes in handen te geven. We laten ons hiervoor inspireren door wat Jan Masschelein en Maarten Simons in hun boek ‘Apologie van de school’ schrijven.
‘…teksten die uitnodigen om anders over opvoeding en onderwijs te denken en te spreken. De nadruk ligt daarbij niet zozeer op de wetenschappelijke onderbouwing en de concrete toepassing maar op de voorgestelde idee.’ (Masschelein & Simons, 2012, p. 2).
We vertrekken vanuit de idee dat ‘leraren (in opleiding) beter in staat zijn om eigenaarschap op te nemen en zo rijke en complete cognitieve schema’s bij kinderen te ontwikkelen, wanneer ze zich verdiepen in leerlijnen en zelf jaarplannen en leerbogen ontwerpen’. We ontwikkelen materialen die het gesprek op gang kunnen brengen. Daarvoor vertrekken we van onze eigen kennis en ervaring en toetsen de ontwerpen af bij een resonantiegroep van vakcollega’s en leraren basisonderwijs. Het is niet de bedoeling dat dit materiaal nadien als een strak keurslijf fungeert. We willen hiermee leraren, studenten en teams uitnodigen om anders over wiskundeonderwijs te denken en te spreken. Het is een vertrekpunt om een discussie op gang te brengen die helpt om een goede opbouw voor wiskunde in de wereld te zetten. Hieronder illustreren we dat idee aan de hand van concrete voorbeelden voor het onderdeel rationale getallen.
Leerlijnen als vertrekpunt
In een eerste stap ontwerpen we voor de verschillende onderdelen van wiskunde, leerlijnen die de verbanden en samenhang in de leerstof verhelderen. Wiskundige inhouden en het wiskundig bouwwerk vormen hierbij het uitgangspunt om een doorgaande lijn te creëren en voor samenhang te zorgen. Afbeelding 9 toont een dergelijke leerlijn voor rationale getallen[4].

Wanneer je de leerlijn bestudeert, zie je een aantal, misschien verrassende, keuzes. Deze keuzes roepen wellicht vragen op. Die helpen om de huidige aanpak, waar we vaak niet meer bij stil staan, opnieuw te overwegen, te bediscussiëren en mogelijk andere keuzes te maken. We lichten hieronder alvast toe waarom wij voor deze opbouw kozen:
- We kiezen ervoor om de leerlijn niet met doelen op te bouwen maar de inhouden te expliciteren. We leggen hiermee de focus niet op het ‘hoe’ maar op het ‘wat’.
- We starten het breukenonderwijs vanuit ‘het dubbel, de helft en een kwart’. Dit onderwerp wordt vaak aansluitend bij de tafels van vermenigvuldigen en delen behandeld (twee keer en gedeeld door twee). Nochtans vormt dit onderwerp de ideale start voor het breukenonderwijs. Het operatorbegrip (ik neem de helft van iets) krijgt bij dit onderwerp op een intuïtieve manier betekenis.
- We kiezen niet (noodzakelijk) voor probleemstellingen vanuit het dagelijkse leven maar gebruiken de opbouw van de wiskunde als opstapje voor nieuwe inzichten. Bijvoorbeeld:
Bij het invoeren van het breukbegrip willen we de kennis die kinderen over delen al opgebouwd hebben verder uitbreiden:
‘Ik kan 8 koekjes verdelen over 4 kinderen. Ieder krijgt er 2. Maar als ik 1 taart heb, hoe kan ik die over 8 kinderen verdelen? En op welke manier kan ik dat deel benoemen en wiskundig noteren?’
Invoeren van kommagetallen:
‘Ik kan op de getallenas (natuurlijke) getallen en breuken plaatsen. Maar die laatste hebben een heel andere schrijfwijze. Bij natuurlijke getallen speelt het getal 10 een sleutelrol (eenheden, tientallen, honderdtallen…), bij breuken is dat niet zo. We zoeken een manier om de breuken zo te noteren dat ze beter passen bij de getallen die we al van vroeger kennen.’
- We nemen niet (enkel) de leerplannen en eindtermen als uitgangspunt om de inhouden vast te leggen. We durven te zoeken naar afgeronde gehelen die relevant zijn voor wiskunde en voor het leren van de leerlingen.
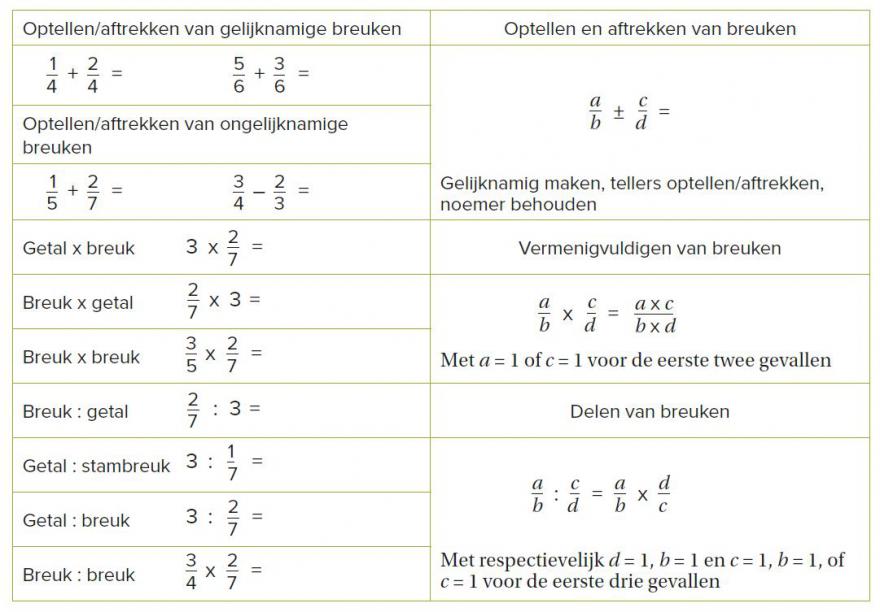
Zo kiezen we ervoor om alle bewerkingen met breuken op het programma te zetten.
Wanneer je de bewerkingen met breuken aanbrengt, bevat dit veel opeenvolgende gevallen (afbeelding 10). Nadat je deze types achtereenvolgens hebt behandeld, kunnen we al deze gevallen herleiden tot drie eenvoudige regels. Het is een prachtige illustratie van de kracht van wiskunde.
Op die manier blijft het onderwerp ‘bewerkingen met breuken’ samen als een relevant geheel binnen het basisonderwijs. Het zorgt er eveneens voor dat leerlingen beter voorbereid zijn om in het secundair onderwijs het rekenen met letters aan te vatten.
- We kiezen voor grote gehelen om de leerlijn op te bouwen: het breukbegrip verwerven (het geheel is benoemd), breuk als rationaal getal (het geheel is de eenheid), breuk als verhouding (vergelijken van breuken als het geheel niet hetzelfde is).
- We brengen structuur aan in opeenvolgende inzichten: breuk nemen van een continu geheel, breuk nemen van een deelbaar aantal en breuk nemen van een ondeelbaar aantal.
Toch hoeden we ons voor te kleine stapjes omdat dan het overzicht verloren gaat: we stappen snel over van stambreuken (breuken met teller = 1) naar echte breuken om de begrippen noemer én teller zo snel mogelijk betekenis te geven.
Jaarplannen met aandacht voor verdieping en herhaling
Vanuit de leerlijnen stelt de leraar een jaarplan op. We vertrekken van een aantal uitgangspunten:
- We kiezen voor een planning met grotere leerstofgehelen om leerlingen de tijd te geven zich grondiger in een onderwerp te verdiepen. We noemen deze leerstofgehelen ‘leerbogen’.
- De leerbogen volgen elkaar functioneel in de tijd op. Zo staat bijvoorbeeld het onderwerp schaal pas na gelijkvormigheid en verhoudingen op het programma. Daardoor ontstaat er vanuit de leerstof automatisch herhaling van de vorige inzichten en worden deze daarbij ingebed in een groter geheel.
- Herhaling is een belangrijk principe om de leerstof vast te zetten. We bouwen regelmatig een herhalingsweek in.
Afbeelding 11 toont een voorbeeld van een uitgewerkt jaarplan voor het zesde leerjaar/groep 8.
Afbeelding 11. Jaarplan zesde leerjaar (groep 8).
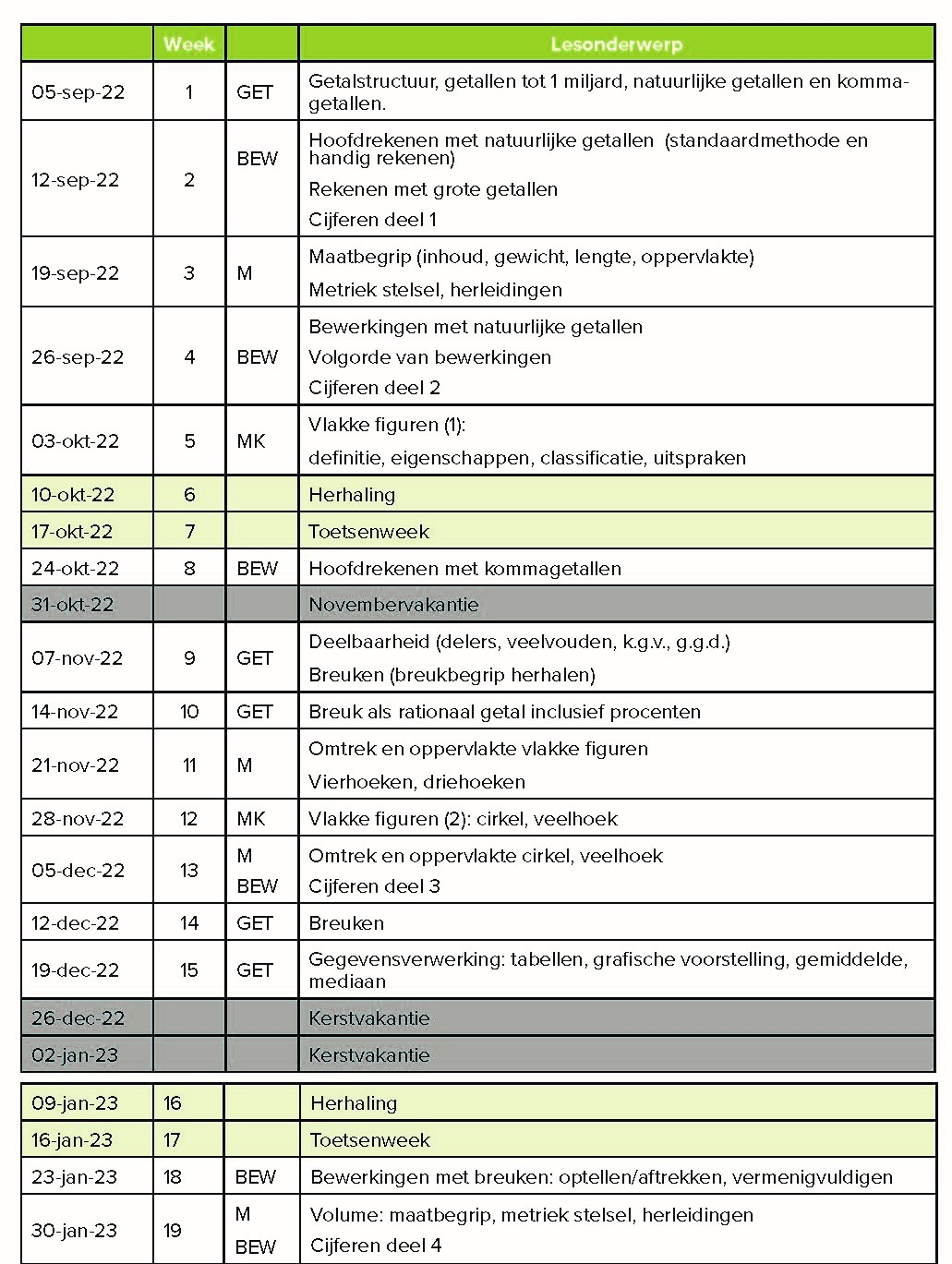
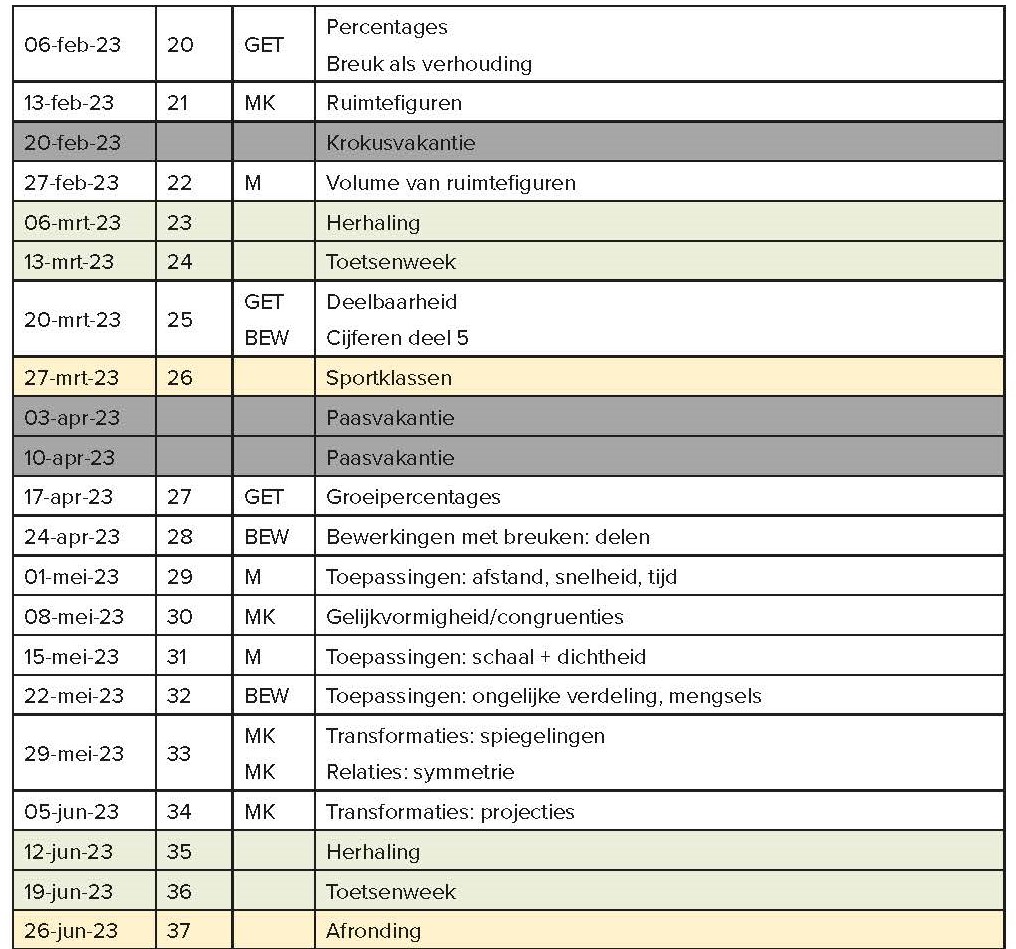
Opnieuw is een jaarplan geen strak keurslijf maar een werkinstrument. Je maakt een plan voordat het jaar start en past het in de loop van het jaar aan in functie van het leren van de kinderen.
Leerbogen van grotere gehelen
Tot slot geloven we dat leerlingen leerstof pas voldoende grondig verwerven, wanneer ze zich langere tijd in de leerstof kunnen verdiepen. Leerbogen zijn grotere leerstofgehelen die over een periode van één à twee weken lopen. We werken zelf enkele leerbogen uit om dit concreet te maken. Ter illustratie vind je enkele fragmenten uit de leerboog ‘Het dubbel, de helft en een kwart’ voor het tweede leerjaar (groep 4).
- Een beknopt overzicht (afbeelding 12) geeft de leraar en de leerlingen duiding hoe de leerstof in de leerlijn past.

- Het eerste deel van elk hoofdstuk bevat de ‘theorie’ of de inzichten die kinderen zullen verwerven. Die wordt stap voor stap uitgewerkt met nadruk op begrijpen hoe de leerstof in elkaar zit. We doen geen suggesties naar werkvorm of organisatie in de klas. Dit geeft een leraar vrijheid. Hij kan zelf kiezen op welke manier hij deze inzichten aanbrengt. Hij heeft immers het meeste zicht op wat er in zijn klas werkt. Afbeelding 13 toont een fragment uit zo’n ‘theoretisch’ stukje.

- We geven de leerlingen een probleemstelling die voortvloeit uit de wiskunde. Afbeelding 14 toont de probleemstelling voor deze leerboog.

- Het tweede deel van het hoofdstuk bestaat uit een aanzienlijke hoeveelheid oefenmateriaal. Het is niet de bedoeling dat de leerlingen alle oefeningen maken. Ook hier kan de leraar zelf beslissen welke opgaven nodig zijn en welke niet. Bovendien kan hij uit deze opgaven putten voor herhalingslessen en toetsen.
- De opgaven zijn geordend in drie reeksen. In reeks 1 vind je opgaven terug die de inzichten uit het instructiemoment herhalen (met andere getallen, met andere voorbeelden) om ze vast te zetten. In reeks 2 worden deze inzichten ingeoefend, waarbij niet-wezenlijke elementen afgewisseld worden. In reeks 3 vind je opgaven waarbij de leerstof gecombineerd wordt met andere inzichten uit de wiskunde. Dit zorgt ervoor dat je als leraar soepel kan differentiëren. Je geeft een klassikale instructie die de basis is voor het leren van alle Kinderen die meer uitdaging kunnen gebruiken, maken meer oefeningen van reeks 3 (afbeelding 15).


- We vertrekken van het principe van het witte blad. We voorzien zo weinig mogelijk voorstructurering (tenzij ruitjespapier) om het denkwerk zo veel mogelijk bij de leerlingen te leggen. Waar we in veel werkboeken merken dat figuren al vooraf verdeeld zijn, kiezen we ervoor om dat niet te doen. Dit zorgt ervoor dat leerlingen zelf ervaren wat het betekent om in ‘gelijke’ delen te verdelen. Dat loopt allicht geregeld fout. Dat ervaren maakt echter deel uit van het worstelen met de leerstof.
- Af en toe voorzien we een opgave die niet opgelost ‘kan’ worden (afbeelding 16). We willen vermijden dat leerlingen het idee krijgen dat wat in het boek staat ook automatisch een oplossing heeft en maar één oplossing. We geven op die manier ook tegenvoorbeelden bij de leerstof die ze leren.
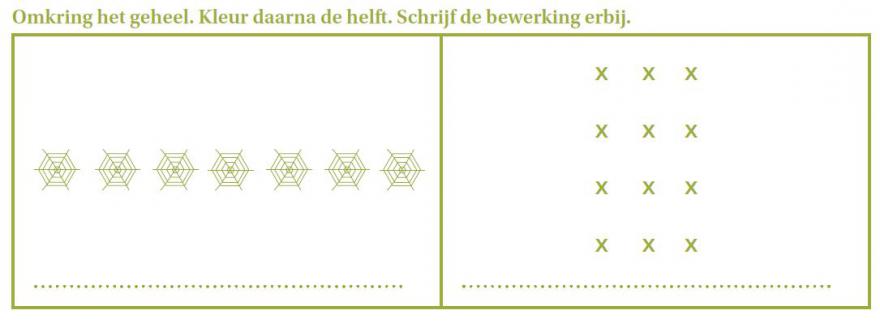
Onderwijs vanuit leerlijnen, jaarplannen en leerbogen
Nadat we onze ideeën en materialen hadden uitgewerkt, wilden we er graag in de praktijk mee werken en zoeken naar mogelijke effecten. We kozen in drie verschillende contexten: met studenten, met lerarenteams en zelf werd ik (Els) voor één jaar wiskundeleraar in het zesde leerjaar/groep 8.
Studenten ontwerpen leerlijnen en leerbogen
In de lerarenopleiding voor het basisonderwijs voorzien we in het tweede opleidingsjaar een vak om rond deze thematiek te werken. De studenten krijgen de opdracht om voor een welbepaald onderwerp eerst een leerlijn voor de basisschool uit te werken, bijvoorbeeld spiegelen. Daarna ontwikkelen ze, voor een specifiek leerjaar, over deze inhoud een leerboog, bijvoorbeeld symmetrische figuren in het zesde leerjaar/groep 8. Tijdens vier werksessies van drie uur krijgen studenten tijd en ruimte om onderling te overleggen en met ons in gesprek te gaan. Het materiaal dat we zelf ontwikkelden, fungeert als voorbeeld.
De studenten worstelen met deze materie. We merken dat ze snel naar leerplannen, eindtermen en werkboeken grijpen. Dat lijkt hun denken eerder te begrenzen in plaats van dat het hen op weg helpt. Deze materialen zetten hen op het ontwerpen van activiteiten zonder dat ze het onderwerp zelf voldoende hebben verkend. Het duurt even voor wij als begeleider dat doorkrijgen. We beseffen dat de eerste hindernis die ze moeten nemen, is dat ze zelf voldoende expertise over het onderwerp verwerven en de essentie van de inzichten die ze kinderen willen bijbrengen, helder krijgen.
Wanneer we het opleidingsonderdeel voor de tweede keer inrichten, wordt dat hun eerste opdracht. Sommige studenten hebben veel weerstand om zich grondig in de inhoud te durven verdiepen. Pas later voelen ze dat dit rendeert. Tijdens de evaluatie klinken er mooie zinnetjes als: ’Ik begrijp nu dat ik eerst zelf goed moet snappen hoe het concept in elkaar zit voor ik kan beginnen nadenken hoe ik het kinderen leer.’ Het maakt duidelijk dat het gemakkelijker is om zelf de touwtjes in handen te nemen als je over voldoende expertise en voldoende rijke cognitieve schema’s beschikt.
Sommige studenten leveren pareltjes van werkstukken in. Tijdens de mondelinge toelichting op het examen klinkt: ‘Ik durf nu zelf na te denken over wat ik uit het werkboek doe en wat ik anders aanpak’, ‘Ik wil mijn lessen herdenken voor ik ze geef’ en ‘Ik voel nu meer vrijheid over wat en hoe ik kinderen iets kan leren’, en ‘Het zou een goede oefening zijn om dit met schoolteams te doen’. Met dat laatste lopen ze voor op onze plannen.
Teams onderzoeken hun praktijk vanuit leerlijnen
Tijdens een aantal nascholingen begeleiden we teams van leraren om hun wiskundeonderwijs te onderzoeken. De leerlijnen voor een welbepaald onderdeel van wiskunde, bijvoorbeeld bewerkingen met natuurlijke getallen, zijn hiervoor het vertrekpunt. De sessie verloopt in twee fasen. Eerst brengen de leraren de leerlijn die ze zelf in hun praktijk gebruiken, in kaart. Zo krijgen ze beter zicht op wat er in de andere leerjaren aan bod komt. Daarna vullen we dit aan met onze eigen leerlijnen en gaan we in op verschillen en gelijkenissen. Dit levert telkens goeie discussies en beslissingen op. We geven hieronder enkele voorbeelden.
De leraar van het vijfde leerjaar/groep 7 ontdekt dat leerlingen in het tweede leerjaar/groep 4 al intuïtief leren compenseren bij het aanleren van de tafels. Zo kan je bijvoorbeeld vermenigvuldigen met negen ook oplossen door bij de gekende tafel van tien, een keertje minder te nemen. Ze ontdekken dat er in de tussenliggende leerjaren vrijwel niets met deze kennis gebeurt. Het is niet verwonderlijk dat in het vijfde leerjaar/groep 7, leerlingen bij het handig rekenen deze strategie als nieuw ervaren. Nieuw plannen rijpen.
In het eerste leerjaar/groep 3 leren kinderen optellen over tien. De leraar geeft aan dat deze materie voor kinderen zeer moeilijk is. Ze gebruikt hiervoor het ‘sok-schema’ (afbeelding 17, boven links). De leraar van het derde leerjaar/groep 5 merkt op dat zij net moeite moet doen om kinderen dit soort notaties af te leren en dat ze veel energie steekt in hen correcte wiskundige notaties aan te leren (afbeelding 17, rechts).

Na een grondige discussie over dit item worden een aantal elementen duidelijk:
- Er is geen twijfel over dat brugoefeningen maken, voor kinderen een moeilijk inzicht is, dat het tijd en moeite vraagt.
- Het is een goed idee om een aangeboden schema kritische te evalueren: helpt het om een inzicht te begrijpen of kost het – zoals hier – vooral moeite om het de kinderen aan te leren. ‘Ik heb me dat helemaal niet afgevraagd’, zegt de leraar van het eerste leerjaar/groep drie met verbazing.
- Dit inzicht ondersteunen met concreet materiaal en een goede verwoording verduidelijken de werkwijze.
- Als we dit combineren met de correcte wiskundige notaties (afbeelding 17 links, onderaan) zorgen we voor een doorgaande lijn in het wiskundeonderwijs. Dit rendeert in de latere leerjaren en zorgt ervoor dat leerlingen beter verbanden zien tussen de opeenvolgende stappen en dat die worden verankerd.
Deze twee voorbeelden illustreren hoe inzicht in leerlijnen en opbouw van het wiskundige bouwwerk, leraren ander keuzes laat maken
Daarnaast valt tijdens deze werksessies op dat leraren het niet gemakkelijk vinden om aan een werkboek/methode zelf aanpassingen te doen. Ook al gaat het soms om eenvoudige dingen zoals twee lessen vervangen door twee andere lessen, lessen groeperen of verschuiven. Gesprek hierover met collega’s en vakexperten helpt om hierin beslissingen te nemen. Ter illustratie lees je hieronder de mail die we nadien ontvingen:
‘Wij leerkrachten van het eerste leerjaar hebben de sprong gewaagd om even de handleiding niet te volgen. Op aanraden van jullie hebben we eerst alle optelsommen tot 6 aangebracht en de volgende dag alle aftreksommen. De overige lessen hebben we deze +/- sommen tot 6 geautomatiseerd. Eerst met materiaal, daarna schematisch en als laatste de kale sommen.
Wat een oefentijd hadden de leerlingen nu! De meeste kinderen waren zéér snel weg met het oplossen van de sommen. Bedankt alvast voor deze nuttige tip! Wijzelf hadden deze sprong nooit durven nemen!’
Als leraren een aantal keer dit soort beslissingen nemen, wordt de drempel lager en durven ze ook meer te onderzoeken of een andere aanpak misschien betere resultaten oplevert. Kwestie van de touwtjes zelf in handen durven nemen.
Een jaar voor de klas in het zesde leerjaar/groep 8
Naast de twee bovenstaande contexten waarin we ons materiaal uitprobeerden, stond ik (Els) samen met de klasleraar, meester Kristof, een heel jaar lang voor de klas in het zesde leerjaar/groep 8. Samen werkten we vanuit een leerlijn een eigen jaarplan uit en ontwierpen we leerbogen. Het was een erg intensief traject waaruit we veel leerden. We geven hier een eerste inkijk in enkele van onze inzichten.
Het jaarplan is een werkinstrument
Al snel werd duidelijk dat wat je plant, niet helemaal is wat er in realiteit gebeurt. Op geregelde tijdstippen stuurden we het jaarplan bij. Voor sommige leerbogen was het nodig om meer tijd uit te trekken (inzicht in breuken), andere leerbogen gingen sneller (volumes van ruimtefiguren).
Al snel merkten we dat langere tijd met leerstof bezig te zijn, aangevuld met herhalingsweken niet genoeg was. Daarom bouwden we kleine herhalingsmomenten in. Elke dag oefende we 10 minuten op de vorige leerstof. Op maandag was dat getallenkennis, op dinsdag bewerkingen, op woensdag meten en op donderdag meetkunde. Vrijdag deden we datzelfde voor Frans.
Leerstof uitdiepen in leerbogen
Het werken met leerbogen gaf meester Kristof en de leerlingen rust. Hij kon een groter geheel voorbereiden waar hij een tweetal weken mee aan de slag kon. Leerlingen kregen tijd om met de leerstof te worstelen, om iets nog niet te kunnen, om samen te zoeken hoe het moet. Tijdens het eerste en tweede lesuur van een nieuwe leerboog waren leerlingen vaak de draad kwijt en struikelden ze over de leerstof. Als leraar kon je dan bijsturen in de lesuren die nog volgden. Dat rendeerde. Tijdens het derde lesuur, vielen de puzzelstukjes vaak op hun plaats. Leerlingen hadden er zichtbaar deugd van dat ze leerstof in de vingers kregen. Dit zorgde voor meer zelfvertrouwen en zelfwaardegevoel én voor meer plezier in wiskunde. Meermaals klonk het zinnetje: ‘Wanneer gaan we hiermee verder?’
Doorheen het jaar zagen we leerlingen steeds beter verbanden leggen tussen de verschillende onderdelen. Zo werd bijvoorbeeld de term ‘recht evenredige grootheden’ een bekend begrip dat leerlingen zelf actief gebruikten. Vanuit ervaringen met ruimtematen (kubieke decimeter) ontdekten ze zelf de formule voor het volume van een balk. Ook al hadden we dat inzicht pas een week later gepland.
Voor differentiatie gebruikten we een eenvoudig model. We startten met een gemeenschappelijke instructie. Leerlingen die de leerstof snel oppikten (groep 2), hielpen tijdens dit onderwijsleergesprek op cruciale plaatsen het proces vooruit. Leerlingen die meer moeite met de leerstof hadden (groep 1), profiteerden hiervan mee. Ze kregen beter zicht op waar we naar toe gingen. Tijdens de zelfstandige verwerking werkten we met twee reeksen oefeningen waarbij we meer inzetten op basisoefeningen voor groep 1 en uitdagende opgaven aanboden voor de andere groep.
We boden voor iedereen leerstof aan buiten de basisdoelen, zoals bijvoorbeeld bewerkingen met breuken. Op de toets maakten we een onderscheid: de meeste vragen behoorden tot de basisleerstof. Daarnaast waren er ook vragen vanuit de differentiatieleerstof. Die werden apart gequoteerd. Leerlingen van groep 2, die geoefend hadden met de differentiatieleerstof, moesten deze opgaven oplossen. De anderen, groep 1, hadden hierin de vrije keuze. Op die manier kregen we zicht in welke mate de leerlingen van groep 2 de differentiatieleerstof effectief ook beheersten en waren die extra opgaven niet vrijblijvend.
Baas boven boek
Voor deze lessen ontwikkelden we zelf materiaal. Dat was veel werk. Maar het zorgde ervoor dat we zelf konden bepalen waar we op inzetten én hoe we dat wilden opbouwen. Zo kozen we er bijvoorbeeld voor om met veel witruimte en een notitieschrift te werken.
Dat was zowel voor ons als voor de leerlingen een leerproces. Afbeelding 18 toont het contrast tussen notities van een leerling in het begin en op het einde van het schooljaar. Vanuit onze voorbeeldfunctie op het bord leerden leerlingen structuur in hun eigen nota’s aan te brengen.


Tijdens de instructie kozen we voor slow teaching. We bouwden stap voor stap het bordplan op (afbeelding 19). Nadien namen leerlingen dit over. Terwijl ze dit overschreven, kregen ze de opdracht om na te denken of ze het goed begrepen hadden. Een tijdje bleef het stil, maar al snel staken verschillende leerlingen hun vinger op en stelden heel boeiende vragen.

De expertise van de leraar
Wanneer we vertellen over dit project krijgen we wel vaker de vraag wat leraren nodig hebben om zo te kunnen werken. Meester Kristof en ik hebben dit geleidelijk aan opgebouwd. In het begin van het schooljaar was het een project van ons beiden, waarbij ik vooral de richting aangaf en materiaal uitwerkte. Naarmate het jaar vorderde verlegden we de focus van mijn inbreng naar die van meester Kristof en experimenteerden we met wat nodig was opdat een leraar dit zelfstandig zou kunnen. We ontdekten dat volgende elementen hierbij kunnen ondersteunen:
- basismateriaal waarin de inzichten die leerlingen moeten verwerven, een ‘theorieboekje’ bijvoorbeeld,
- een rijke set van oefeningen van verschillend niveau waaruit een leraar kan kiezen,
- werkboeken die volgens hoofdstukken opgebouwd zijn, in plaats van volgens individuele lessen,
- een gesprekspartner die als kritische vriend fungeert.
Volgend jaar zal meester Kristof samen met de leraar van het vierde leerjaar/groep 6 dit traject voor getallenkennis en bewerkingen doorlopen.
Besluit
In dit artikel werkten we drie grote elementen uit. Vanuit observatie ervaarden we dat leerlingen arme en weinig samenhangende cognitieve schema’s voor wiskunde ontwikkelen. Inzetten op de expertise van leraren, durven de basisdoelen te overschrijven, leraren ruimte geven om opnieuw met hun kerntaak bezig te zijn en leraren helpen om baas boven boek te zijn, kunnen hier een impact op hebben. We gingen aan de slag met leerlijnen, jaarplannen en leerbogen en ontdekten dat je hiermee leraren anders kan laten kijken naar hoe je goed wiskundeonderwijs in de wereld zet. Dit soort materiaal geeft de leraar opnieuw de touwtjes in handen om het leren van de kinderen te sturen en te zorgen voor beter onderwijs. De leraren en leerlingen die hiermee experimenteerden waren alvast enthousiast.
Als we op het project terugkijken, zijn er twee belangrijke dingen die boven komen drijven. Het is nooit te laat om wiskundige feeling bij kinderen te ontwikkelen. En hoe heerlijk is de vrijheid die je als leraar voelt wanneer je zelf de touwtjes in handen hebt bij het aansturen van leren van de kinderen![5]
[1] In het basisonderwijs wordt de wiskundige term ‘rationale getallen’ vaak vervangen door de combinatie ‘breuken, kommagetallen en percenten’. Dit zijn verschillende notaties voor hetzelfde rationale getal.
[2] Voorheen door peilingsproeven bij een steekproef van leerlingen, vanaf 2023 – 2024 met de Vlaamse toetsen voor de hele populatie.
[3] Een prisma is een veelvlak dat begrensd wordt door twee evenwijdige veelhoeken met eenzelfde vorm en grootte (grond- en bovenvlak) en waarvan de opstaande zijvlakken parallellogrammen zijn.
[4] In deze leerlijn vind je de bewerkingen met kommagetallen niet terug. Die werkten we in de leerlijn bewerkingen-hoofdrekenen uit. Dit omwille van de analogie met de bewerkingen met natuurlijke getallen
[5]Voor dit project ontwikkelden we een leerboog van het dubbel, de helft en een kwart. Interesse? Neem contact op met els.vanemelen@ucll.be. Ook andere reacties of feedback zijn welkom.
Mathematics is a beautiful construction. Based on that premise, we set up practical research over the past two years. Through observations in classes and conversations with teachers and teacher-teams we learned that pupils develop incomplete cognitive constructs for mathematics. We identified possible causes.
Based on that analysis, we hypothesized: ‘If teachers know their curriculum well, design coherent annual plans themselves, and offer the subject matter in larger clusters to the pupils, clout to have pupils develop rich and complete cognitive constructs.’ We used the mathematical structure itself as a base to design materials that teachers can use to reflect on and redesign their practices.
We tested this thinking and these materials ourselves by teaching during a hole year a class of sixth graders (last year of primary school) for mathematics. We also presented this way of thinking and these materials to student teachers and teams of teachers. It triggered rich discussions, that supported teachers to make different choices and thus improve their math education.
Literatuur
Brinckman, P., & Versluys, K. (2021). Naar de kern: de leerlingen en hun leer-kracht. Brussel: Departement Onderwijs en Vorming. Opgehaald van https://onderwijs.vlaanderen.be/sites/default/files/2021-10/RAPPORT-OK19%20oktober.pdf
De Man, L. (2022). Naar een kwaliteitsalliantie. Brussel: Departement Onderwijs en Vorming. Opgehaald van https://www.vlaanderen.be/publicaties/naar-een-kwaliteitsalliantie
Drijvers, P., Van Streun, A., & Zwaneveld, B. (2019). Handboek wiskundedidactiek. Amsterdam: Epsilon uitgaven.
Masschelein, J., & Simons, M. (2012). Apologie van de school. Leuven: Uitgeverij Acco.
Schmeier, M. (2019, Januari 23). Onderwijsvernieuwers willen de breuken afschaffen. NRC. Opgehaald van https://www.nrc.nl/nieuws/2019/01/23/onderwijsvernieuwers-willen-de-breuken-afschaffen-a3651355
Schmeier, M. (2021). Bordwerk en aantekeningen, slow teaching in de 21e eeuw. Huizen, Nederland: Pica.
Tersago, G., Boel, A., & Lievens, A. (2009). Nieuwe Tal-rijk Werkboek 6A. Mechelen: Plantyn.
Van Emelen, E. (2019). Is de lat voldoende om erover te springen. Uitwiskeling, 35(3). Opgeroepen op juni 14, 2023, van https://www.uitwiskeling.be/2019/08/06/is-de-lat-voldoende-om-erover-te-springen/?v=d3dcf429c679
Van Emelen, E. (2020, mei 16). De kracht van een leerboog. Basis, 127/05. Opgehaald van https://www.hetacv.be/docs/default-source/acv-csc-docsitemap/6000-centrales/6770-christelijk-onderwijzersverbond-cov/6850-basis/basis-2020/basis-5/leerkracht-5.pdf?sfvrsn=5ae7f8de_2
Van Emelen, E. (2022, Herfst). Grootschalig toetsen. Uitwiskeling. Opgehaald van https://www.uitwiskeling.be/2022/10/01/grootschalig-toetsen/?v=d3dcf429c679
Vlaamse overheid. (sd). Onderwijsdoelen en leerplannen in het basisonderwijs. Opgeroepen op juni 14, 2023, van Vlaanderen - onderwijs en vorming: https://onderwijs.vlaanderen.be/nl/onderwijsdoelen-en-leerplannen-in-het-basisonderwijs
Vlaamse overheid. (sd). Onderwijsdoelen wiskunde. Opgeroepen op juni 14, 2023, van Onderwijsdoelen: https://onderwijsdoelen.be/resultaten?onderwijsstructuur=LO&filters=onderwijsniveau%255B0%255D%255Bid%255D%3Df7dcdedc9e9c97a653c7dba05896ef57a333480b%26onderwijsniveau%255B0%255D%255Btitel%255D%3DBasisonderwijs%26onderwijsniveau%255B0%255D%255Bwaarde%255D
Zwik, M. (2019, Juni 13). Tekstarm... Opgehaald van Blogcollectief Onderzoek Onderwijs: https://onderzoekonderwijs.net/2019/06/13/tekstarm/
Zwik, M. (2020, februari 18). Tekstrijk. Opgehaald van Blogcollectief Onderzoek Onderwijs: https://onderzoekonderwijs.net/2019/06/13/tekstarm/
