Breuken in een breder perspectief
EDB
In het onderwijs is er steeds meer aandacht voor de rol van basisvaardigheden in de dagelijkse praktijk en beroep. Toepasbaarheid van wat op school geleerd is dan ook steeds vaker een onderwerp voor discussie. Er bestaat een beeld van geringe toepasbaarheid van breuken, bovendien wordt het rekenen met breuken als moeilijk ervaren. Is er dan nog een plek voor breuken in het curriculum, of betekent de geringe toepasbaarheid dat je hier vooral op het formele rekenen moet focussen voor met name de leerlingen die doorstromen naar havo en vwo?
Deze beelden zijn aanleiding voor dit artikel waarin de concepten verbonden aan breuken worden onderzocht in de doorgaande leerlijn. Er wordt daarbij ook nadrukkelijk gekeken naar die toepasbaarheid, waarbij ook andere schoolvakken in beeld komen. Dit levert een ander beeld op met nieuwe vragen voor de invulling van het curriculum. Deze manier om breder naar breuken te kijken, kan meer algemeen een waardevolle bijdrage leveren aan de discussie over basisvaardigheden.
Inleiding
Het onderwerp breuken is om verschillende redenen bijzonder. In de lesstof staan breuken op de drempel tussen basisonderwijs en voortgezet onderwijs. In de referentieniveaus zijn de breuken onderdeel van twee domeinen: getallen & bewerkingen en verhoudingen. Dat breuken in meerdere categorieën thuishoren betekent een risico. Algemeen betekent een verdeling over categorieën dat er makkelijk iets tussen wal en schip kan vallen. Eerder onderzoek naar breuken (Bruin-Muurling, 2010) liet al zien dat ‘de breuk als een deling’ en ‘delen door een breuk’ daar voorbeelden van zijn. Breuken hebben daarnaast de reputatie het eerste rekenconcept in het curriculum te zijn dat zo abstract is, dat het lastig uit te leggen is. Tot slot lijken breuken bijna niet in ons dagelijks leven (meer) voor te komen. Zelden zie je een breuk als $\frac{3}{7}$ in het straatbeeld; we hebben het over 400 gram gehakt en niet over $\frac{2}{5}$ kilo.
Breuken hebben dus een risicovolle plek in de doorgaande lijn van het curriculum en worden gezien als ingewikkeld, abstract of formeel en met schijnbaar weinig praktische toepassing. Er lijkt soms zelfs een angst voor (het rekenen met) breuken te zijn ontstaan en er is bij herhaling discussie over óf, en in welke mate breuken nog in het curriculum thuishoren. Keijzer (2023) schetst een beeld van twee conclusies die aan de gering geachte toepasbaarheid van breuken worden gekoppeld. Aan de ene kant is de geringe toepasbaarheid een argument om het onderwerp nog verder uit het curriculum te schrappen. Aan de andere kant is de geringe toepasbaarheid argument om een onderwerp als breuken in het curriculum te behouden maar juist veel formeler aan te bieden. Dat maakt dit onderwerp niet alleen interessant van zichzelf, maar hierdoor past het ook in de voortdurende discussie over basisvaardigheden.
In onderwijs en beleid is er een toenemende aandacht voor het functionele aspect van het rekenen: de relatie met de werkelijkheid. In het mbo vormt functionele gecijferdheid de basis voor de nieuwe rekeneisen die sinds schooljaar ‘22/’23 worden gebruikt. In het concept voor de nieuwe kerndoelen po en onderbouw vo is ‘wiskunde en de wereld’ een apart domein. Deze aandacht volgt internationale trends op dit gebied. Het sluit aan bij het nadenken over hoe het gebruik van rekenen en wiskunde verandert in de maatschappij en wat dit voor het onderwijs betekent. Op haar beurt voedt deze ontwikkeling de discussie over wat dan die basis is waarover leerlingen moeten beschikken om zich in die wereld te redden: welke (formele) beheersing van rekenvaardigheden is nodig? Een discussie die vaak in uitersten en gepolariseerd wordt gevoerd.
Als je iets verder inzoomt, valt op dat er bij het beoordelen van de (praktische) bruikbaarheid van breuken een sterke focus is op het formele en de rekenregels. Dan gaat het dus om (formele) breuken, herkenbaar als getallen in de breuknotatie. Verder lijkt er vooral gezocht te worden naar toepassingen waar de breuk vrij ‘letterlijk’ voorkomt. Inderdaad komen we in het dagelijks leven de notatie van twee natuurlijke getallen boven elkaar met daartussen een breukstreep nog maar zelden tegen, met enkel uitzonderingen als $\frac{1}{2}$ of $\frac{3}{4}$. Met de focus op de formele rekenregels lijkt bovendien het belang van het rekenen met breuken nog vooral voor die leerlingen te bestaan die doorstromen naar het vwo (en eventueel havo), waar zij binnen het vak wiskunde met breuken rekenen in de algebra, kansrekening of goniometrie. Daarmee wordt het beeld bevestigd dat je de zwakkere rekenaars niet met breuken moet vermoeien. In het mbo, met de sterke focus op het functionele aspect van rekenen én het toestaan van de rekenmachine bij alle berekeningen, is het dan ook begrijpelijk dat docenten zich afvragen of er nog plek is voor formeel rekenen zoals dat met breuken gebeurt.
Tegenover het tot een minimum beperken van het rekenen met breuken staat, dat je bij het maken van een samenhangende leerlijn niet onder het begrijpen van de aan breuken verbonden concepten uit lijkt te komen. Het rekenen met procenten, verhoudingen of samengestelde grootheden kan bijvoorbeeld niet zonder begrip van gelijkwaardigheid. Deze onderwerpen vormen een aanzienlijk deel van het rekencurriculum van het po, in de referentieniveaus én de nieuwe rekeneisen voor het mbo. De toepasbaarheid van breuken lijkt daarbij dus in ieder geval in secundaire zin voor álle leerlingen groot.
De tegenstellingen in bovenstaande schets zijn aanleiding om in dit artikel breuken vanuit een ander perspectief te analyseren: de rol van de concepten die aan breuken verbonden zijn in het onderwijs dat op het basisonderwijs volgt. In dit perspectief staan de conceptuele kant van breuken, lange doorlopende leerlijnen en de toepassing van reken-wiskundige vaardigheden centraal. Ik begin met een korte samenvatting van literatuur over breuken waarbij ik inga op de verschijningsvormen en ambiguïteit. Daarna zet ik een aantal aan breuken verbonden concepten op een rij. Daarvoor kies ik een meer formele insteek door eerst naar de definitie van- en rekenregels voor rationale getallen te kijken. Daarna verschuift de analyse naar de onderwerpen verhoudingen en procenten, waar ik onderzoek hoe de breukenconcepten hierin verweven zijn. Ik sluit de analyse af met een selectie van toepassingsvoorbeelden uit een variëteit van schoolvakken en daarmee toepassingsgebieden.
De veelzijdigheid van breuken
In de vakdidactiek over breuken wordt uitgegaan van vijf subconstructen. Hiermee wordt als het ware een indeling gemaakt in de verschijningsvormen van breuken: ‘part-whole’, ‘measure’, ‘quotient’, ‘ratio number’ en ‘multiplicative operator’ (e.g. (Behr, Wachsmuth, Post, & Lesh, 1984; Kieren, 1980; Streefland L. , 1983). Naar het Nederlands vertaald betekent dit dat er onderscheid wordt gemaakt tussen de breuk als een ‘deel van een geheel’, een ‘maat’, een ‘deling’, een ‘getal dat een verhouding weergeeft’ en als een ‘multiplicatieve factor’. In het werk van bijvoorbeeld (Streefland L. , 1991) komen deze subconstructen naar voren als het resultaat van een brede fenomenologische inbedding (Freudenthal, 1983) en worden ze gebruikt om de breuk ‘veelsporig’ te introduceren aan de hand van passende contexten. Streefland kiest er daarna voor om vanuit deze veelsporige verkenning, het begrip eensporig op te trekken naar een meer formele beheersing van de rekenregels voor breuken.

Ambiguïteit
De subconstructen zijn een illustratie van de veelzijdigheid van breuken. De indeling wekt soms de indruk dat je in een specifieke context een eenduidig label kunt hangen aan de betekenis van het breukensymbool. Ten onrechte, want je kunt niet concluderen dat er per context maar één betekenis is; de subconstructen representeren geen scheidbare betekenissen van breuken. De subconstructen zijn wél een illustratie van de rijke ambiguïteit (Byers, 2007; Bruin-Muurling, 2010). Met ambiguïteit wordt bedoeld dat in één wiskundig concept meerdere perspectieven samenkomen; zelfs versmelten. Je kunt die verschillende perspectieven los beschrijven maar nooit los van elkaar zien. Je kunt hooguit zeggen dat een of meerdere perspectieven dominant zijn in een bepaalde context. $\frac{2}{3}$ kilo suiker is een voorbeeld van een ‘multiplicative operator’, maar tegelijkertijd is deze breuk ook een measure gerelateerd aan 1 (kilo). Om een wiskundig concept echt te begrijpen zijn alle perspectieven nodig. Dat alleen is echter niet voldoende. De perspectieven moeten bovendien versmolten zijn tot één begrip. De veelzijdigheid is daarom niet alleen van belang bij de inbedding (multiple embodyment), ook na de introductie is de samenhang tussen alle perspectieven belangrijk om ze tot één te laten versmelten.
Proces-object dualiteit
Een ambiguïteit die vaak voorkomt is die van de dualiteit tussen proces en object. Sfard (1991) beschrijft hoe, als je de geschiedenis van het ontstaan van wiskunde bestudeert, opvalt dat nieuwe concepten en constructen vaak eerst naar voren komen als processen. Pas later worden ze geaccepteerd als een object waar je weer verder over kunt redeneren en waarop weer nieuwe wiskunde wordt gebouwd. Rationale getallen zijn daar net als de negatieve getallen een voorbeeld van. Negatieve getallen bijvoorbeeld ontstonden uit het aftrekken van twee natuurlijke getallen (0,1, 2, …). Eerst werden ze nog als een ‘tekort’ gezien waar verder mee gerekend moest worden. Dat tekort was een tussenstap, maar in eerste instantie géén uitkomst. Pas later werden de tekorten als getallen beschouwd, die de uitkomst van een berekening konden zijn én waarmee gerekend kon worden. Het werden dus ‘dingen’. Zo’n overgang tussen proces en object wordt ook wel reïficatie (verdinglijking) genoemd, een idee dat ook al voorkomt in het werk van Dewey (1933)en Freudenthal (1983). Sfard betoogt, net als Dewey en Freudenthal, dat elke leerling opnieuw de stappen doorloopt die ook in de geschiedenis van de wiskunde werden doorlopen, uiteraard nu versneld. Zij ziet een parallel tussen die momenten in de ontwikkeling van de wiskunde waar deze haperde of waarover wiskundigen aanvankelijk van mening verschilden en die onderdelen die voor leerlingen lastig zijn. Sfard constateert dat reïficatie dit soort lastige blikwisselingen in het denken van wiskundigen markeert. Ook bij de rationale getallen is sprake van proces-object dualiteit. De rationale getallen ontstaan uit de bewerking ‘delen’. In de paragraaf over de rationale getallen ga ik hier dieper op in.
Ambiguïteit in de breedte
Nu is proces-object dualiteit niet de enige ambiguïteit waar je in het leren van breuken mee te maken hebt. Je hebt ook te maken met de verschillende perspectieven. Bij proces-object overgangen komt het proces meestal voor het object. Bij ambiguïteit die om de verschillende perspectieven gaat, kun je niet op die manier in termen van volgorde van concepten spreken. Je ziet dat bijvoorbeeld terug in verschillende manieren om breuken te introduceren. Zo kun je het begrip van breuken, zoals in Nederland wordt gedaan, introduceren aan de hand van ‘deel-geheel’, bijvoorbeeld door te werken met cirkeldiagrammen (taarten) waarvan een deel gekleurd is. Een andere introductie van breuken komt voort uit ‘delen’; 6 taarten kun je eerlijk verdelen over 3 mensen en deze deling kun je noteren als $\frac{6}{3}$, zo kan je ook 2 taarten eerlijk verdelen over 3 mensen (2 ÷ 3 wordt geschreven als $\frac{2}{3}$). Als laatste voorbeeld kunnen breuken geïntroduceerd worden als maat. Als je met de helen niet precies kunt meten, heb je een nieuwe, kleinere eenheid nodig die ontstaat door de hele in gelijke delen te verdelen.
Hoewel ambiguïteit een krachtige beschrijving geeft van wiskundige concepten, kan het soms ook het gevoel oproepen dat je onnodig moeilijk aan het doen bent. Het is goed je daarbij te realiseren dat hier een verschil bestaat tussen de leerling die net aan een onderwerp begint en de docent voor wie de verschillende perspectieven al versmolten zijn. Op het moment dat het niveau van begrip bereikt is, is het lastig om nog los over de perspectieven te spreken zonder een gevoel van trivialiteit. Zo zou je bij het voorbeeld van de te verdelen taarten al in termen van een verhouding kunnen denken, terwijl het voor de leerlingen in deze introductie echt nog gaat om eerlijk delen. Ik vermoed dat ambiguïteit de reden is dat het niet lukt de onderlinge relatie tussen de subconstructen empirisch goed in beeld te brengen, en niet een gebrek aan onderzoeksinzet zoals Purnomo et al (2021) suggereren.
Hoewel de subconstructen erg nuttig zijn om de volle breedte van het concept breuken te overzien, zijn ze als analysemiddel minder geschikt. Je belandt immers telkens in een discussie (met jezelf) dat de breuk op dat moment ook bij andere subconstructen hoort. In de verdere analyse heb ik daarom gekozen om, met de verschillende perspectieven in het achterhoofd, te focussen op de conceptuele ideeën die ten grondslag liggen aan breuken. De volgende stap is daarom om vanuit een meer formeel en wiskundig perspectief naar de definitie van rationale getallen te kijken. Dit is nadrukkelijk een theoretische verkenning van het concept breuken.
Rationale getallen
Voor we beginnen met een analyse van de rationale getallen is een korte noot op zijn plek. Breuken en rationale getallen worden vaak als synoniem gezien, die zienswijze klopt niet helemaal. Rationale getallen kunnen altijd als breuk geschreven worden, dus in een breuknotatie staan, maar dat hoeft niet. Veelal verschijnen ze als een kommagetal, ook wel decimale breuk genoemd.
De breuk is niet alleen een schrijfwijze voor een rationaal getal. De breuk staat ook voor de notatie van een deling. Bij de breuk als notatievorm hoeven de tellers en noemers niet altijd gehele getallen te zijn. Denk aan formules als $\frac{(-b±√b^2-ab)}{2a}$ (abc-formule voor het oplossen van 2e graads vergelijkingen) en $\frac{1}{r}$ = $\frac{1}{b}$ + $\frac{1}{v}$ (de lenzenformule) waarin vaak met kommagetallen wordt gewerkt. Maar ook aan irrationale getallen als $\frac{√3}{2}$ (goniometrie). In formules zorgt de breuk notatie voor visuele structuren die het rekenen vergemakkelijken. De notatie als (-b±√b2-4ab) ÷ 2a) maakt bijvoorbeeld vereenvoudigen, het herkennen van de symmetrie-as van de parabool of het verder rekenen met het antwoord, veel lastiger.
Een rationaal getal is de verhouding tussen twee gehele getallen; ratio is een ander woord voor verhouding. De rationale getallen kunnen worden gedefinieerd als equivalentieklassen van paren van gehele getallen. Twee geordende paren (a,b) en (c,d) zijn gelijkwaardig als a × d = b × c. Je noemt dit de equivalentie relatie. In de rekendidactiek hebben we het over gelijkwaardige breuken ($\frac{2}{3}$ = $\frac{8}{12}$) of over gelijkwaardige verhoudingen (‘5 van de 10’ is gelijkwaardig aan ‘1 van de 2’).
Een rationaal getal is dus de verhouding tussen 2 getallen. Bijvoorbeeld 3 staat tot 4 of als ‘3 van de 4’. In de context kan het gaan om de verhouding tussen twee elementen (3 delen verharder ‘op’ 4 delen hars) of om een deel van een geheel (3 rode knikkers ‘van de’ totaal 4 knikkers). $\frac{3}{4}$ als een deel van een geheel betekent 3 delen van $\frac{1}{4}$, ofwel $\frac{1}{4}$ + $\frac{1}{4}$ + $\frac{1}{4}$ = 3 × $\frac{1}{4}$ = $\frac{3}{4}$. De breuk is ook een deling: $\frac{3}{4}$ = 3 ÷ 4. Deze 3 manieren om tegen de breuk aan te kijken vragen om perspectiefwisselingen. Bij ‘3 van de 4’ is 4 als het ware het geheel waarvan we 3 elementen kiezen. Bij ¾ (deel van een geheel), speelt 1 de rol van het geheel, maar is ook $\frac{1}{4}$ een eenheid. En bij 3 ÷ 4 starten we met 3 helen die in 4 stukken wordt verdeeld.
Door de equivalentie is de uitkomst van de deling, de factor tussen beide delen in de verhouding. Dat wil zeggen: $\frac{3}{4}$ is de factor tussen de teller 3 en noemer 4. Dus 4 × $\frac{3}{4}$ = 3 én 3 ÷ $\frac{3}{4}$ = 4. In de gelijkwaardigheid tussen (a,b) en (c,d) ligt zelfs nog een factor verscholen. Dit laat zich het beste uitleggen met een afbeelding van een vergroting. De getallenparen (5,6) en (10,12) zijn gelijkwaardig, want 5 × 12 = 6 × 10. De interne verhouding bij de getallenparen is $\frac{5}{6}$. We zagen deze factor al: 6 × $\frac{5}{6}$ = 5 en 12 × $\frac{5}{6}$ = 10, ofwel d x $\frac{a}{b}$ = c. Er is ook een externe factor die de relatie tussen de getallenparen vastlegt. Elke afmeting uit het linker plaatje wordt 2 keer zo groot in het rechter plaatje: 5 × 2 = 10 en 6 × 2 = 12. De externe factor is $\frac{c}{a}$, en er geldt b x $\frac{c}{a}$ = d.
Figuur 2: interne en externe verhouding
De rationale getallen vormen een verzameling in een rijtje van steeds grotere, geneste getallenverzamelingen:
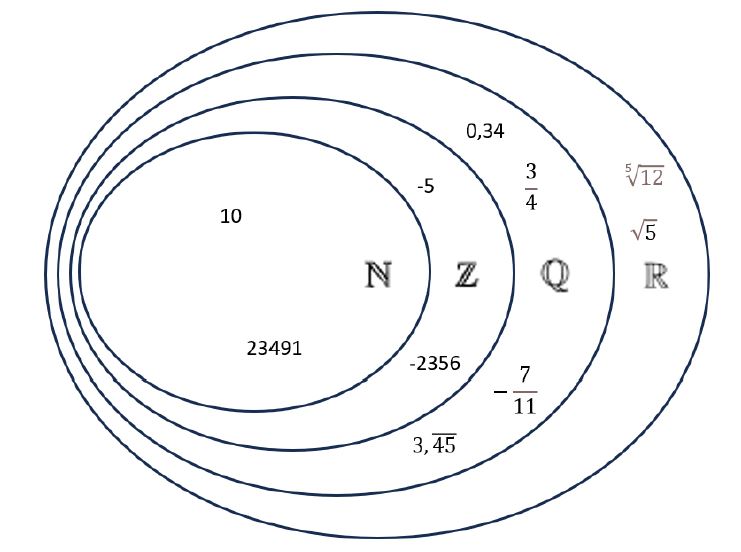
Figuur 3: natuurlijke getallen, gehele getallen, rationale getallen en reële getallen
Je zou kunnen zeggen dat elke volgende verzameling een ‘probleem’ oplost. Zoals al besproken bij proces-object dualiteit, lossen de rationale getallen het probleem op dat een deling van twee gehele getallen niet altijd een geheel getal is. Binnen de verzameling van de rationale getallen geldt immers wél dat een rationaal getal gedeeld door een rationaal getal weer een rationaal getal is. Dit zorgt ervoor dat de deling een bijzondere positie inneemt bij de rationale getallen.
De getallenverzamelingen zijn niet alleen een uitbreiding van getallen. Bij elke uitbreiding de getallenverzameling krijgen de (basis)bewerkingen +, -, × en ÷ een uitgebreidere betekenis. Het gaat bij de uitbreiding dus niet alleen om de getallen zelf, maar ook om hoe je met deze objecten rekent. Denk maar aan de nieuwe betekenis voor aftrekken bij de negatieve getallen: 7 - - 3. Deze nieuwe betekenis van de basisoperaties in Q kan formeel beschreven worden met de rekenregels:
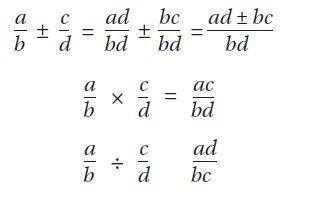
In deze schets van de rationale getallen en de basisbewerkingen zijn een aantal breukenconcepten naar voren gekomen:
Bij deze rekenregels komen nieuwe concepten naar voren. Bij het optellen (en aftrekken) moeten de breuken gelijknamig worden gemaakt. Dat is een concept dat nieuw is voor de rationale getallen. Je kunt dit concept koppelen aan maatverfijning. De stambreuken $\frac{1}{b}$ en $\frac{1}{d}$ vormen als het ware nieuwe eenheden. Zonder gelijke eenheden kunnen de breuken niet worden opgeteld. Door de breuken te vertalen naar breuken met de nieuwe gezamenlijke eenheid $\frac{1}{bd}$, kan dit wel. Bij het vermenigvuldigen maak je gebruik van de betekenis ‘vermenigvuldigen als oppervlakte’ en daar wordt de betekenis van ‘een deel van’ iets nemen aan toegevoegd: ‘$\frac{2}{3}$ × 450’ lees je als ‘$\frac{2}{3}$ deel van 450’. De betekenis van delen is voor de natuurlijke getallen: verdelen (Hoeveel krijgt ieder?) of afpassen (Hoe vaak past het erin?). Dit worden in de vakdidactiek ook wel de verdelings- en verhoudingsdeling genoemd, hoewel ook hier geldt dat je door de ambiguïteit geen strikt onderscheid tussen deze twee kunt maken. Soms wordt aan het delen met hele getallen ook al de betekenis van het terugrekenen naar de één(heid) toegevoegd: ‘Een verpakking van 3 ballen kost € 6. Wat kost 1 bal?’. Bij breuken blijken verdelen en afpassen slechts van beperkte geschiktheid. Hoewel het verdelen nog wel betekenis kan geven aan een som als $\frac{4}{5}$ ÷ 2 (bijvoorbeeld $\frac{4}{5}$ taart verdelen over 2 mensen) wordt dat ingewikkeld als er gedeeld wordt door een breuk. Ook het afpassen biedt weinig betekenis als de deling niet uitkomt op een geheel getal; wat doe je met de rest bij ‘Hoeveel stukken van $\frac{2}{3}$ meter kun je halen uit 2 $\frac{1}{3}$ meter?’. De betekenis van terugrekenen naar de één(heid) kan wel in al die situaties gebruikt worden, maar kom je minder vaak tegen. Bij het delen lopen sommige leerlingen er overigens tegenaan dat zij onterecht het idee hebben dat een deling altijd kleiner maakt. Tot slot is er nog een andere betekenis die gebruikt kan worden om de rekenregels voor delen te begrijpen: de relatie tussen delen en vermenigvuldigen. Al eerder beschreef ik de blikwisseling tussen deel-geheel en delen: 3 × $\frac{1}{4}$ = 3 ÷ 4. Je kunt ook van de deling een keersom maken: 3 ÷ $\frac{2}{5}$ = … is het zoeken naar het getal waarvoor geldt dat … × $\frac{2}{5}$ = 3. Dus: … × $\frac{2}{5}$ × $\frac{5}{2}$ = 3 × $\frac{5}{2}$ = … . Daarentegen is ‘delen door een breuk is vermenigvuldigen met het omgekeerde’ voor veel leerlingen een regel waarbij ze geen verbinding leggen met-, en dus geen begrip hebben van de tegengestelde bewerkingen keer en delen.
In deze schets van de rationale getallen en de basisbewerkingen zijn een aantal breukenconcepten naar voren gekomen:

Figuur 4: Concepten verbonden aan breuken
Breuken en verhoudingen en procenten
In voorgaande beschrijving is een wat formele insteek en formulering gekozen om de concepten scherper te kunnen verwoorden. Deze keuze is ingegeven door de aard van deze eerste analyse. Nu volgt de vraag hoe de hierboven beschreven concepten zich manifesteren in de verschillende onderwerpen uit het curriculum. We starten bij de onderwerpen waarvoor breuken een fundering vormen, en waarin ze niet altijd herkenbaar zijn in een breuknotatie. Je kunt hier denken aan verhoudingen en procenten. Deze rekenonderwerpen hebben een breed toepassingsgebied in andere vakken, de beroepspraktijk en het dagelijks leven. In al deze toepassingsgebieden mag met de rekenmachine gerekend worden, waardoor de rekenregels zelf niet altijd gekend hoeven te worden en er ook op andere manieren gerekend kan worden.
Verhoudingen
Heeft een kaart een schaal van 1 : 100, dan betekent dat dat de afstanden op die kaart $\frac{1}{100}$ deel van de werkelijkheid zijn. Er is een vaste verhouding tussen de kaart en de werkelijkheid. Je gebruikt hier het begrip dat ‘$\frac{1}{100}$ deel van iets’ hetzelfde is als ‘delen door 100’, of als ‘vermenigvuldigen met 0,01’. Er bestaat hier gelijkwaardigheid tussen de getallenparen gevormd door de afstand op de kaart en de bijbehorende afstand in werkelijkheid: bijvoorbeeld (12 cm, 1200 cm) en (5 cm, 500 cm). Deze getallenparen zijn ook gelijkwaardig met de schaalnotatie 1 : 100. Je maakt dus weer gebruik van de eigenschap dat d x $\frac{a}{b}$ = c. Die factor $\frac{1}{100}$ is omkeerbaar: als je vanuit de kaart de afstanden in de werkelijkheid wilt berekenen dan vermenigvuldig je met 100. $\frac{1}{100}$ is het omgekeerde van 100. Je kunt hier spelen met het omgekeerde én de tegengestelde bewerkingen. Dus A ÷$\frac{1}{100}$ = A ×100 en B ÷ 100 = B × 0,01. Gelijkwaardige verhoudingen blijken voor veel kinderen heel intuïtief. Zo intuïtief dat het een vraag oproept over de volgorde van concepten in de didactische opbouw: is een verhouding (bijvoorbeeld schaal) een toepassing van al eerder opgedaan breuken begrip, of juist een ingang tot het rekenen met breuken.
Een ander voorbeeld van het rekenen met verhouding vind je bij het berekenen van medicatie; een onderdeel van het medisch rekenen in het mbo. Bij medicijnen waarbij de werkzame stof is opgelost, wordt de concentratie meestal genoteerd als de verhouding tussen het aantal ml vloeistof in bijvoorbeeld de ampul en het totaal aantal mg medicijn in die ampul. Je noemt die verhouding in dit geval de concentratie. Bij apotheekbereidingen wordt op het etiket de concentratie volgens een vast format vermeld (NVZA, 2004); bijvoorbeeld FUROSEMIDE 20 mg = 2 ml (10 mg/ml). Je kunt op verschillende manieren rekenen met dit soort concentraties.
In een ampul Gentreks van 2 mL zit 80 mg werkzame stof. Er moet 70 mg Gentreks worden toegediend. Hoeveel mL moet je toedienen?
Manier 1:
- Per mL is er 80 ÷ 2 = 40 mg aanwezig is.
- Benodigd aantal mL: 70 mg ÷ 40 mg/mL = 1,75 mL
Manier 2:
· Er is $\frac{70}{80}$ deel van de werkzame stof in de hele ampul nodig.
· Dus: $\frac{7}{8}$ deel van 2 mL = 1,75 mL.
Weten waarom je moet delen door 40 mg/mL in de eerste berekening, kunnen rekenen met de verhouding van manier 2 of begrijpen wat beide berekeningen met elkaar te maken hebben, vragen om begrip. In manier 1 moet je begrijpen dat de ‘concentratie’ (hier 40 mg/mL) de factor is tussen de hoeveelheid werkzame stof en de hoeveelheid vloeistof. De concentratie is de breuk met de hoeveelheid werkzame stof in de teller, en de hoeveelheid vloeistof in de noemer. Bij manier 2 wordt gebruik gemaakt van een andere factor: de breuk 70 mg van de 80 mg ofwel $\frac{7}{8}$ deel. En daarom is er $\frac{7}{8}$ deel van de ampul nodig.
Verschillende concepten uit figuur 4 komen in deze voorbeelden terug. De vraag is of deze conceptuele kennis van breuken onmisbaar is of dat dit soort berekeningen ook gedaan kunnen worden zonder (informele) kennis van breuken. In lesmateriaal zie je voorbeelden dat het rekenen met breuken en het begrip daarvan omzeild wordt. Er wordt dan een meer procedurele didactiek gebruikt. Dit is niet anders dan bij andere onderwerpen waarin breuken voorkomen. Voor het rekenen met de rekenmachine lijkt dit voldoende. Het interessante is, dat in die gevallen de breuken toch niet helemaal weg te denken zijn, bijvoorbeeld als de breuknotatie wordt gebruikt om de deling op te schrijven. Dat zie je bij het rekenen met medicatie bijvoorbeeld door gebruik te maken van een formule als $\frac{V}{A}$, waarbij V de gevraagde hoeveelheid medicijn is en de A aangeeft hoeveel medicijn er per ml aanwezig is (e.g. Het vraagt dat de student de breuk als een notatie van een deling moet (her)kennen.
Procenten
Ook procenten bouwen voort op breuken. In de kern zijn procenten breuken met als noemer 100. Je maakt hier voortdurend gebruik van equivalentie: je zet een verhouding tussen hoeveelheden om naar een verhouding met daarin de 100 als geheel. Als je uit moet rekenen hoeveel procent ‘15 van de 300’ is, dan zet je als het ware die verhouding om naar de equivalente verhouding 5 van de 100, ofwel 5%. In breukentaal zou je kunnen zeggen dat je hier zowel teller als noemer deelt door 3:
$\frac{15}{300}$ = $\frac{15÷3}{300÷3}$ = $\frac{5}{100}$. We zagen dit gebruik van een factor tussen de getallenparen al in het voorbeeld van de vergrotingen.
Met lastiger getallen zoals ‘11 van de 275’ reken je niet met mooie factoren uit jouw getalrelatie-netwerk. Je gaat nu direct over naar een deling: $\frac{11}{275}$ van 100% =
11 ÷ 275 × 100% = 4%. Hier gebruik je dus dat de verhouding als breuk geschreven kan worden en reken je met de breuk, door deze als deling te interpreteren.
Reken je een percentage van een hoeveelheid uit, bijvoorbeeld 17% van 450 = 76,5, dan betekent 17% hetzelfde als $\frac{17}{100}$ deel. Weer gelijkwaardige verhoudingen: 0,17 is niet alleen de factor tussen 17 en 100, maar ook tussen 76,5 en 450.
Bij het terugrekenen naar 100%, zoals dat typisch gebeurt bij het berekenen van een prijs zonder BTW, wordt het begrip van wat je aan het doen bent extra beproefd. Hier is het startpunt immers niet meer de 100%. Je moet als het ware $\frac{100}{121}$ deel uitrekenen. Een inzicht dat dit soort berekeningen eenvoudiger maakt, is dat het bedrag inclusief BTW 1,21 keer het bruto bedrag is. Hier reken je terug en wordt de vermenigvuldiging omgekeerd in een deling (÷ 1,21). Het rekenen met factoren is een belangrijke stap in het leren rekenen met procenten. Het maakt bijvoorbeeld het terugrekenen naar 100%, het berekenen van rente op rente en het redeneren met procenten makkelijker.
Breuken in andere vakgebieden
Een aanzienlijk deel van de referentieniveaus rekenen en de nieuwe rekeneisen in het mbo is verbonden aan de onderwerpen verhoudingen en procenten. De analyse in de vorige paragraaf laat de rol van breukenconcepten daarin zien. Op deze manier spelen de breuken een belangrijke, minder zichtbare rol in het wiskundecurriculum van de onderbouw van het vo en het generieke rekenen in het mbo. Om ook een indruk te krijgen van de rol in andere schoolvakken, neem ik nog een laatste stap in mijn analyse. Hiervoor heb ik een aantal voorbeelden geselecteerd uit eindexamens van verschillende vakken op verschillende niveaus, omdat deze los staan van specifieke lesmethodes en de daarin gevolgde didactiek. Ik heb hier het vak wiskunde buiten beschouwing gelaten hoewel voorbeelden daarin talrijk zijn, bijvoorbeeld in de goniometrie, kansrekening, analyse en algebra. Deze voorbeelden zijn bekender. Ze vragen vaak een beheersing zonder rekenmachine en hierbij gaat het dan ook om de formele beheersing van de rekenregels.
In deze analyse streef ik niet na om een uitputtende lijst van toepassingen op te stellen. De gekozen voorbeelden zijn een illustratie van de omvang en veelzijdigheid van de toepassing van breuken en de daaraan verbonden concepten. Vervolgonderzoek zou naar een veel completere lijst toe kunnen werken. Hierin zouden dan ook voorbeelden uit het mbo meegenomen kunnen worden. Deze zijn hier niet opgenomen. Hier hebben we slechts een indruk van omdat onderwerpen uit vakken als economie in het mbo in het beroepsrekenen terugkomen. Deze laatste stap moet dus vooral gezien worden als een vingeroefening, een proof of concept.
Samengestelde grootheden
Samengestelde grootheden die gevormd worden als de verhouding tussen twee grootheden kom je op veel verschillende plekken in het curriculum tegen. We kwamen ze ook al tegen in het medicatie voorbeeld. Hieronder zijn natuurkundige contexten uit een vmbo examen en havo examen naast elkaar gezet:
_w880.jpg)
Wat opvalt aan deze voorbeelden is dat de samengestelde grootheden op een andere manier worden genoteerd, terwijl er op vergelijkbare manieren mee gerekend wordt. Links wordt door het woord ‘per’ meer een link gelegd met gelijkwaardige verhoudingen. Je zou ‘per’ ook kunnen zien als het terugrekenen naar de een(heid). Links zie je de breuk terug in de eenheden. Rechts is de breuk zichtbaarder en heeft het de betekenis van een deling. Hier wissel je van perspectief tussen de breuk als een deling én de uitkomst van die deling. De uitkomst van die deling is de factor tussen de twee enkelvoudige grootheden. Bij dit soort samengestelde grootheden heb je als het ware te maken met een drietal: de stookwaarde is één getal dat berekend kan worden door de totale energie door het totaal aantal kilo te delen.
Algemeen kan de derde waarde uitgerekend worden als de andere twee bekend zijn: als a = $\frac{b}{c}$ dan geldt dat b = a × c en c = $\frac{b}{a}$.
Snelheid
Snelheid is een bijzondere samengestelde grootheid, waar leerlingen al vroeg mee kennismaken. Snelheid krijgt vaak het karakter van één getal alsof het een enkelvoudige grootheid is. Hierdoor hebben veel leerlingen niet door dat je twee snelheden niet zomaar kunt middelen.

Figuur 6: VWO wiskunde C – 2011 – 2e tijdvak
Zo kan je in deze opgave niet zeggen dat de gemiddelde snelheid $\frac{4}{9}$ × 120 + $\frac{5}{9}$ × 60 » 86,67 km/uur is. Een juiste berekening staat in het correctievoorschrift onder de opgave. De tijd staat in de noemer van snelheid. Bij het combineren van de trajecten moet dus rekening gehouden worden met de verhouding tussen de tijden, in plaats van de verhouding tussen de afstanden. Je kunt overigens wel zeggen dat de gemiddelde snelheid $\frac{2}{7}$ × 120 + $\frac{5}{7}$ × 60 » 77 km/uur is.
Ratio
Niet altijd hoeft gerekend te worden met de breuk. In plaats daarvan moet er geredeneerd worden over de grootte van de ratio zoals de volgende voorbeelden laten zien.
_w880.jpg)
Demografische druk is een economische term die ook in het aardrijkskunde curriculum voorkomt. Het is de verhouding tussen het totaal aantal mensen jonger dan 20 jaar of ouder dan 65 jaar en het aantal mensen tussen de 20 en 65 jaar oud, en geeft een indruk van de verhouding tussen het niet werkende en werkende deel van de bevolking. De opgaven vragen om een globale redenering over de invloed van een verandering in de teller en de noemer op de uitkomst van de deling. Rechts bijvoorbeeld is in tekening 2 Va kleiner dan in tekening 1, terwijl Q gelijk blijft. Dat betekent dat de ratio kleiner wordt.
Kansen
Bij opgaven over erfelijkheid wordt met breuken gerekend zoals onderstaand voorbeeld laat zien.

Figuur 8: : VWO 2023 – eindexamen biologie – tweede tijdvak
Om de kans te berekenen kan een compleet schema van mogelijkheden worden gemaakt en het aantal gewenste genotypes ten opzichte van het totaal aantal mogelijkheden worden berekend (deel-geheel). De vlinders hebben elk 4 mogelijkheden om hun genen door te geven. In totaal zijn er 16 mogelijkheden waarvan er 2 het gewenste genotype zijn. De kans is $\frac{2}{16}$ = $\frac{1}{8}$. Er kan hier ook een andere insteek gekozen worden. Dan worden kansen met elkaar vermenigvuldigd zoals je dat ook mag doen met het werpen van twee dobbelstenen. At kan alleen met een kans $\frac{1}{2}$ vanuit vlinder 1 komen, B alleen met een kans van $\frac{1}{2}$ van vlinder 1 en G alleen van vlinder 2 met een kans van $\frac{1}{2}$. De kans op het gevraagd genotype is dus $\frac{1}{2}$ × $\frac{1}{2}$ × $\frac{1}{2}$ = $\frac{1}{8}$. Bij dit soort opgaven is vereenvoudigen (equivalentie) en het vermenigvuldigen van breuken nodig. Bij het rekenen met kansen kan er over het algemeen uit deze twee genoemde aanpakken gekozen worden: het vermenigvuldigen van de kansen versus het tellen van de gewenste mogelijkheden als deel van het totaal aantal mogelijkheden. Het begrijpen hoe deze twee perspectieven zich tot elkaar relateren en wanneer welke methode handiger is, vraagt eveneens om begrip van breuken.
Indexcijfers
Indexcijfers worden gebruikt in het vak economie of in het mbo bij commerciële calculaties. Indexcijfers zijn een andere manier om procenten aan te geven. Kenmerkend is dat indexcijfers vaak over meerdere jaren worden gecombineerd en dat er vaak buiten het basisjaar (indexcijfer 100) wordt gerekend. In dit voorbeeld is de consumentenprijsindex (CPI) van twee verschillende jaren gegeven en moet een procentuele prijsstijging binnen die periode worden berekend:
Op de site van het CBS staat:
CPI2020 = 107,51
CPI2022 = 121,43
In de periode 2021-2022 is een prijsstijging van 10% berekend.
Wat is de prijsstijging in de periode 2020-2021?
Hier heb je te maken met een stijging over een stijging. De prijsstijging tussen 2020- 2022 is 121,43/107,51 » 1,1295. Dus: 1,1295 = prijsstijging 20-21 × 1,10. Dat betekent prijsstijging 20-21 is ongeveer 1,0268, ofwel een stijging van 2,68%. In een berekening als deze ben je constant bezig met deel-geheel berekeningen; meer specifiek breuken die worden geschreven als decimale getallen.
Bij het berekenen van het reëel rentepercentage gebeurt iets interessants. De indexcijfers fungeren als deel-geheel verhouding. Aan het einde van de berekening moet van deze verhouding weer een indexcijfer gemaakt worden door te vermenigvuldigen met 100:
Reëel indexcijfer = (nominaal indexcijfer / prijsindexcijfer) × 100
Bij een rentepercentage van 0,9% en een inflatie van 4% betekent:
reëel indexcijfer = (100,9 / 104) × 100 » 97,0
Lenzenformule
In het vak natuurkunde wordt met de lenzenformule ($\frac{1}{r}$ = $\frac{1}{b}$ + $\frac{1}{v}$) gerekend. In deze oude examenopgave vind je daarvan een voorbeeld.

Figuur 9: : VWO – Natuurkunde – 2e tijdvak – 2005
Over het algemeen wordt hier gewoon met de rekenmachine gerekend. Uit v =28 mm en f = 45 cm volgt dat $\frac{1}{b}$ = $\frac{1}{28}$ - $\frac{1}{450}$. Dat de breuken hier niet gelijknamig zijn is op de rekenmachine geen probleem, dit worden kommagetallen door 1 door 28 en daarna 1 door 450 te delen. Je vindt 1/b door deze kommagetallen van elkaar af te trekken. Om b = 29,9 mm uit te rekenen moet je nu dit getal omkeren. Hiervoor moet je begrijpen dat 1 ÷ $\frac{1}{b}$ = b. Daarna wordt de verhouding tussen b en v en de diameter van de bloem in werkelijkheid gebruikt om uit te rekenen dat op film deze diameter 0,59 cm is ($\frac{29,9}{450}$ = $\frac{diameter beeld}{8,9 cm}$). De rekenregels voor optellen en aftrekken zijn hier dus niet nodig, hoewel de formule dat wel doet vermoeden. In plaats daarvan wordt van de breuk als deling gebruik gemaakt.
Conclusies en discussie
In dit artikel heb ik de breuk en de concepten die daarbij horen in een breder perspectief getrokken. Ik wilde daarbij breder kijken dan de meer formele vaardigheden, een perspectief breder dan normaal wordt meegenomen in discussies over basisvaardigheden. Deze verkenning bestond uit 4 stappen: een korte beschrijving van relevante perspectieven uit de vakdidactische literatuur over breuken, een analyse van de concepten verbonden aan rationale getallen, het gebruik van deze concepten bij de onderwerpen verhoudingen en procenten en tot slot een selectie van examenopgaven uit verschillende examenvakken van verschillend niveau. De verkenning in dit artikel leverde een aantal inzichten op.
In de eerste stap kwam naar voren dat er bij het onderwerp breuken sprake is van veel ambiguïteit. Niet alleen ontstaan de rationale getallen uit het proces van delen (proces-object dualiteit). Tegelijkertijd komen veel verschillende perspectieven in het concept samen. In de voorbeelden later in het artikel valt op dat de breuk als een deling en ook de breuknotatie als een algemene notatie voor delen, veel wordt gebruikt. Het is de vraag in hoeverre de inbedding van dit perspectief in het huidige onderwijs voldoende is. Deel-geheel lijkt het dominante perspectief in de introductie van breuken in het curriculum. Hier zou verder onderzoek wenselijk zijn. In 2010 bleek immers dat toen het begrip van de breuk als deling bij leerlingen laag was (Bruin-Muurling, 2010).
In het algemeen is niet alleen de veelzijdigheid van concepten interessant, maar juist ook de perspectiefwisselingen die bij ambiguïteit horen. Bij de verdere analyse van breuken springt de blikwisseling tussen de breuk als één geheel en als twee losse delen in het oog. Bij het rekenen met samengestelde eenheden speelt dit een rol, waar bijvoorbeeld de concentratie de factor werd tussen werkzame stof en hoeveelheid vloeistof. Bij de grootheid snelheid, lijken de twee losse delen vaak zelfs niet meer zichtbaar.
Ambiguïteit, ofwel de versmelting van perspectieven, maakt een beschrijving op basis van subconstructen ingewikkeld. Een kader van onderliggende concepten met de ambiguïteit op de achtergrond, is daarvoor veel geschikter. Uit de analyse van rationale getallen en de rekenregels is een lijst van zulke concepten naar voren gekomen. De lijst van concepten lijkt een afspiegeling te zijn van de concepten die vervolgens in de analyse van procenten en verhoudingen en daarna van breuken in andere vakken naar voren kwamen. Deze aanpak lijkt dus een geschikt kader op te leveren om een beter beeld te krijgen van hoe in de breedte van het curriculum een beroep wordt gedaan op de concepten verbonden aan breuken.
De analyse laat zien dat we voor de toepasbaarheid van breuken op twee niveaus moeten kijken. Aan de ene kant zijn er breukenconcepten die de fundering vormen voor andere onderwerpen. Het rekenen met factoren bij procenten is daar een voorbeeld van: moet je de factor bepalen waarmee je a moet vermenigvuldigen om b te krijgen, dan gebruik je het inzicht dat a x $\frac{b}{a}$. De breuk is hierin vooral van belang als onderliggend concept en is minder zichtbaar als breuk zelf. Aan de andere kant heeft de analyse ook laten zien dat breuken ook nog steeds herkenbaar voorkomen als een getal met teller en noemer waarmee gerekend moet worden. Denk hierbij aan de erfelijkheidskansen of de lenzenformule. Niet alleen dat: het voorbeeld van de demografische druk en Va/Q ratio laten zien dat er ook globaal over de grootte van de ratio geredeneerd moet kunnen worden. De breukenconcepten hebben dus zowel een indirecte, minder zichtbare toepassing als een directe, zichtbare.
In mijn analyse lag de focus op vakinhoudelijke aspecten. Om dit te beschrijven heb ik een aanpak en taal moeten gebruiken die niet altijd direct geschikt is voor een aanpak voor leerlingen. Die vertaalslag is een belangrijke stap die nog moet worden gemaakt. Daarom wil ik deze discussie afsluiten met een aantal vragen die deze analyse oproept voor de didactiek in de lange doorlopende leerlijn.
Het lijkt erop dat er in de praktijk van het huidige curriculum soms om conceptueel begrip heen wordt gewerkt, door in te zetten op een procedure of stappenplan. Dat gebeurt zowel in het reken- en wiskunde onderwijs als in de vakken waar deze kennis wordt toegepast. Je kunt dan bijvoorbeeld denken aan het kruisproduct, de beroemde 2, 3, 6 driehoek of een formule voor procentuele toename. De vraag is of dit ‘om de breuken concepten heen werken’ een goede didactische oplossing is. Je zou kunnen zeggen van wel. De breuken worden immers door velen als ingewikkeld gezien, en als er een mogelijkheid zou kunnen zijn ze niet te gebruiken, dan zou dat een mogelijke oplossing bieden. Waarom zou je het dan nog ingewikkeld maken door zo op de concepten in te zoomen. Aan de andere kant lijkt het wegpoetsen nooit helemaal te lukken. Zo wordt de notatie met een schuine of horizontale breukstreep bijna achteloos als de notatie voor delen gebruikt. Het is interessant om te onderzoeken of leerlingen hierbij de connectie met breuken leggen als er niet is gewerkt aan een conceptuele basis.
Nog fundamenteler is de vraag is of het inzetten op conceptueel begrip aan het begin van de leerlijn al dat andere rekenen veel eenvoudiger en inzichtelijker kan maken. In plaats van bij de moeilijke punten in de leerlijn lokale didactische oplossingen te zoeken, kan je er immers ook voor pleiten dat je het probleem daar moet aanpakken waar het ontstaat: bij de basis, bij het begrijpen. Kan investeren in begrip aan het begin uiteindelijk zorgen voor minder problemen later? En zou dat uiteindelijk niet tot een hoger beheersingsniveau kunnen leiden met minder inspanning?
Het nadeel van zo’n lokale oplossing is immers dat, als deze eenmaal bestaat, het de gangbare didactiek wordt. Er wordt dan niet meer nagedacht of dit in de lange doorlopende leerlijnen wel een wenselijke aanpassing of oplossing was. Een concept als breuken verdwijnt dan bijvoorbeeld steeds meer uit het zicht omdat deze weggepoetst wordt, waaruit de conclusie kan worden getrokken dat ze niet meer in het basiscurriculum thuishoort. Een bijkomend, averechts effect op de inhoud van het curriculum.
Juist dit soort analyses, van de lange doorlopende leerlijn, inclusief de toepassing in andere vakken en een theoretische verkenning, kunnen een check zijn of de juiste concepten aan de orde komen.
Een laatste didactische vraag is wat het betekent om ook wezenlijke veranderingen in de context van het reken-wiskunde en wiskundeonderwijs mee te nemen. Deze veranderingen hebben zowel invloed op de inhoud van het curriculum als op de didactiek. Veranderingen in hoe de wiskunde in onze maatschappij wordt gebruikt en de nieuwe hulpmiddelen die beschikbaar zijn in het ‘leven na school’, betekenen dat er ruimte is en moet komen voor andere doelen. Waar vroeger in de didactiek nadruk lag op het met begrip aanleren van hoe je bepaalde berekeningen uit moet voeren (zoals bijvoorbeeld in het werk van Streefland en breder ook RME), wordt dat rekenwerk in de praktijk van nu vaak overgenomen door rekenapparaten. Het betekent niet dat je bepaalde basisvaardigheden niet meer hoeft te bezitten. Het betekent wel dat er iets anders wordt verwacht van leerlingen en studenten. Je moet er rekening mee houden dat we nu te maken hebben met andere doelstellingen dan waar in eerder onderzoek en werk op het gebied van breuken van werd uitgegaan. Dat betekent mogelijk ook dat je tot nieuwe conclusies komt op basis van onderzoek. In de voorbeelden wordt bijvoorbeeld duidelijk dat het gebruik van de rekenmachine een game-changer is. Deels betekent dit dat de breuken omgezet worden naar kommagetallen en dat er kortere strategieën mogelijk zijn voor het rekenen met verhoudingen en procenten. Hiervoor moet dan wel begrip ontstaan over het rekenen met factoren en hoe zo’n factor verbonden is aan de verhouding tussen de delen.
Ofwel dat een groei van 50 naar 130 overeenkomt met een factor van $\frac{130}{50}$ = 2,6. Ofwel een stijging van $\frac{80}{50}$ = 160%. Ook dit is een aspect dat in een vervolgonderzoek naar de toepassing van breuken in langere doorlopende leerlijnen meegenomen zou kunnen worden.
In de discussie over de basisvaardigheden mis ik vaak de doorgaande leerlijn, de echte verbinding met andere vakken en een analyse van het indirecte gebruik van onderliggende concepten. In dit artikel heb ik laten zien wat een breder perspectief op kan leveren en hoe het beeld van het belang van bepaalde basisinzichten daarmee kan veranderen. Mijns inziens is zo’n bredere insteek, waarbij niet alleen naar de vaardigheden wordt gekeken, maar ook naar de onderliggende concepten, noodzakelijk voor een gezonde discussie over de basisvaardigheden. Tot slot denk ik dat we mogen concluderen dat breuken een grote toepasbaarheid hebben voor álle leerlingen.
There is a growing attention to the role of basic mathematical skills that students need in their daily and professional life. Practical use of topics learned at school is therefore increasingly a topic for debate. In this article fractions are analyzed, since they are perceived to be of limited applicability. Being a topic that is hard for many students, provokes the question to limit its role in the curriculum. The analysis takes a different standpoint: how are the concepts linked to fractions used in the long run of mathematics education and applied in other school subjects. This broader perspective shows the varied and frequent application of these concepts. The analysis leads to new questions for curriculum change in both fractions as well more generally in other basic skills.
Literatuur
Behr, M., Wachsmuth, I., Post, T., & Lesh, R. (1984). Order and equivalence of rational numbers: A clinical teaching experiment. Journal for Research in Mathematics Education, 15(5), pp. 323-341.
Bruin-Muurling, G. (2010). The development of proficiency in the fraction. . Eindhoven: Technische Universiteit Eindhoven.
Byers, W. (2007). How mathematicians think: using ambiguity, contradiction, and paradox.
Dewey, J. (1933). How we think. . Buffalo, New York: Prometheus books.
Examens, C. v. (2022). Biologie VWO - Syllabus centraal examen 2024.
Freudenthal, H. (1983). Didactical Phenomenology of mathematical structures.
Keijzer, R. (2003). Teaching formal mathematics in primary education. Fraction learning as mathematising process.
Keijzer, R. (2023). Conceptueel kijken naar breuken. Volgens Bartjens – ontwikkeling en onderzoek, 42(5), pp. 51-65.
Kieren, T. (1980). The rational number construct - its elements and mechanisms. In Recent research on number learning (pp. 125-150). ERIC/SMEAC.
Megens, M. (2014). Verpleegkundig rekenen. Opgehaald van https://www.youtube.com/watch?v=Gor0Uz9bNRU
NVZA, W. E. (2004). Richtlijn etikettering van apotheekbereidingen.
Purnomo, Y. W. (2021). Learning trajectory based on fractional sub-constructs: Using fractions as quotients to introduce fractions. Mathematics Teaching-Research Journal, 13(3), pp. 183-207.
Sfard, A. (1991). On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational studies in mathematics, 22(1), pp. 1-36.
Streefland, L. (1983). Aanzet tot een nieuwe breukendidactiek volgens wiskobas. Utrecht: Vakgroep onderzoek wiskunde onderwijs.
Streefland, L. (1991). Fractions in Realistic Mathematics Education, a paradigm of pevelopmental research. Dordrecht: Kluwer Academic Publishers.
