‘Probeer het maar!’ Leraren-in-opleiding onderwijzen algebraïsch redeneren

Onze analyse toont een gemengd beeld. Leraren-in-opleiding blijken goed in staat om een les te ontwerpen met de informele leeromgeving van de hangmobiel. Ook hun studenten of leerlingen kunnen hier goed mee uit de voeten. Tegelijkertijd wordt de stap van het mathematiseren vaak overgeslagen door de leraren-in-opleiding. Dit onderschrijft het belang voor de lerarenopleiding om het concrete informele handelen als basis van formeler reken-wiskundig redeneren voldoende te blijven benadrukken.

 

Inleiding

In dit artikel bekijken we de relatie tussen de inhoud van een les die leraren-in-opleiding aangeboden krijgen op de lerarenopleiding, de vertaling die ze van deze lesinhoud naar hun stageschool maken, en de reflectie die ze hier vervolgens zelf op geven in een volgende bijeenkomst op de opleiding. We doen dit binnen de context van algebraïsch redeneren – een onderwerp dat niet expliciet terugkomt in het reguliere curriculum van de basisschool – en preciezer: het oplossen van (informele) lineaire vergelijkingen.

Doorlopende leerlijnen van het primair onderwijs naar het voortgezet onderwijs zijn binnen het reken-wiskundeonderwijs een voortdurend punt van aandacht. Naast aandacht voor de doorgaande lijnen in leerstofinhouden als breuken en verhoudingen, is een belangrijke rol in die aansluiting weggelegd voor wiskundige activiteiten zoals probleemoplossen en redeneren (SLO, 2023). Het stimuleren van algebraïsch redeneren kan worden gezien als een manier om bezig te zijn met zowel redeneren over relaties en het oplossen van problemen, als met de inhoudslijn van verbanden en verhoudingen. Door al op de basisschool te starten met het aanbieden van activiteiten die informeel algebraïsch redeneren van leerlingen bevorderen, kan de basis gelegd worden voor de in het voortgezet onderwijs aangeboden formelere algebra. In eerder onderzoek (Otten, 2020) bekeken we hoe algebraïsch redeneren bij leerlingen van groep 7 op een informele manier uitgelokt kan worden. We ontwikkelden hiertoe een ‘hangmobiel’ (afbeelding 1), een fysiek balansmodel met aan weerszijden van een horizontale balk twee kettingen met balletjes van verschillende gewichten die gemakkelijk verplaatst kunnen worden. De verdeling van de balletjes over de hangmobiel kan gezien worden als een fysiek gerepresenteerde en informele vergelijking met onbekenden. Leerlingen kunnen verschillende handelingen uitvoeren om het model in balans te houden of die juist te verstoren. Hiermee beginnen ze het proces van mathematiseren, van informeel handelen en manipuleren in de werkelijkheid naar schematisch representeren en uiteindelijk formeel noteren (vgl. Treffers, 1987). Door de uitwerking van hun handelingen op de balans van het model te voelen en te zien en deze percepties te verklaren (vgl. Lakoff & Nunez, 2000), leren leerlingen op een informele wijze over het algebraïsche begrip gelijkheid (Bush & Karp, 2013) en over algebraïsche strategieën om deze gelijkheid te behouden, zoals herstructureren, isoleren of substitueren. Bij herstructureren wordt bijvoorbeeld de volgorde van de onbekenden of balletjes aan één kant veranderd of de twee kanten helemaal omgewisseld. Bij isoleren wordt door aan beide kanten hetzelfde gedaan waardoor er minder onbekenden overblijven. En bij substitueren wordt door een bekende relatie toe te passen een aantal onbekenden of balletjes vervangen door andere. Het werken met de hangmobiel kan zo de basis leggen voor het oplossen van contextgebonden en formele vergelijkingen (zie ook Otten et al., 2019).

 

Context: Minor Rekenexpert

In navolging van haar promotieonderzoek gaf Mara Otten als gastdocent jaarlijks een gastles aan leraren-in-opleiding van de Minor Rekenexpert aan de HAN Nijmegen. Deelnemers aan deze minor zijn derdejaars studenten van de pabo en studenten van de opleiding tot tweedegraads leraar wiskunde voortgezet onderwijs. Leraren-in-opleiding lopen stage in het primair onderwijs, voortgezet onderwijs of op het MBO.

In de eerste bijeenkomst, verzorgd door hun eigen rekendocent, lossen leraren-in-opleiding (stelsels van) informele en formele vergelijkingen op en krijgen ze les over de didactiek hiervan. De balansmethode voor het oplossen van vergelijkingen wordt hierbij besproken. Leraren-in-opleiding oefenen zelf met het oplossen van vergelijkingen, bijvoorbeeld de formele vergelijking 3a + 24 = 5a + 16, waarbij ze bij elke stap aan moeten geven welke strategie van de balansmethode ze gebruiken: herstructureren – bijvoorbeeld links en rechts in de vergelijking omdraaien; isoleren – bijvoorbeeld gelijke variabelen aan beide kanten van de vergelijking weghalen om een andere variabele te isoleren; en substitueren – bijvoorbeeld een variabele vervangen door een andere variabele of waarde. Vervolgens komt de hangmobiel als voorbeeld van een fysiek balansmodel ter sprake. Leraren-in-opleiding bespreken met elkaar bepaalde kenmerken van dit model, zoals de relatie tussen actie en perceptie: de handelingen die uitgevoerd worden en het al dan niet in balans komen van het model, maar ook het belang van de open vragen die het onderzoekende karakter van de activiteiten bepalen. Aan het eind van deze bijeenkomst krijgen leraren-in-opleiding de opdracht mee om zelf een les met dit fysieke model te ontwerpen. Ze bereiden de les voor via een lesbeschrijvingsformulier en filmen waar mogelijk de les. In de tweede bijeenkomst reflecteren de leraren-in-opleiding onder begeleiding van de gastdocent met elkaar op hun gegeven lessen.

 

Focus van dit artikel

In dit artikel reflecteren we vanuit twee verschillende perspectieven op hoe leraren-in-opleiding aan de slag zijn gegaan met deze opdracht en een les hebben ontworpen en uitgevoerd. In de eerste plaats bekijken we hoe leraren-in-opleiding een lesontwerp vormgeven en de les uitvoeren na het bijwonen van een bijeenkomst over de balansmethode en de fysieke hangmobiel op de lerarenopleiding. Hiervoor beschrijven we de door hen geformuleerde lesdoelen, welke invulling ze geven aan de les en welke aspecten ze uitlichten tijdens de reflectie na afloop van de les op de opleiding. Dit resulteert in zicht op hoe leraren-in-opleiding informatie van de lerarenopleiding vertalen naar hun stagepraktijk. In de tweede plaats borduren we voort op eerder onderzoek (Otten, 2020) naar de potentie van de leeromgeving – waarin een belangrijke rol is weggelegd voor mathematiseren, open en onderzoekend leren en fysieke ervaringen – bij basisschoolleerlingen. In dit artikel bespreken we deze potentie bij een bredere doelgroep en kijken we in hoeverre de leraren-in-opleiding daar gebruik van maken in hun lesaanbod.

 

Deelnemers

In dit artikel bespreken we het werk en de reflectie daarop van vijf leraren-in-opleiding van de Minor Rekenexpert van de HAN:

• Anna loopt stage op het mbo niveau 2 en niveau 3
• Ietje loopt stage in ‘groep 9’ van een brugschool
• Jons voert deze opdracht uit met een bijlesleerling uit de derde klas van vmbo-basis
• Lianne loopt, net als Ietje, stage in ‘groep 9’ van een brugschool
• Rick loopt stage in jaar 2 van het vmbo-KGT

We beginnen met een beschrijving en analyse van de lesdoelen zoals deze vijf leraren-in-opleiding die hadden geformuleerd in hun lesvoorbereiding. Ook analyseren we het uiteindelijke lesverloop. Vervolgens gaan we hier verder op in aan de hand van de reflecties van twee leraren-in-opleiding op hun uitgevoerde lessen.

 

Wat waren de lesdoelen van de vijf leraren-in-opleiding en welke opdracht geven ze hun leerlingen/studenten?

Het valt op dat de meeste leraren-in-opleiding tenminste één van hun lesdoelen formuleren rondom het oplossen van de vergelijking. Zo formuleert Jons het lesdoel: ‘[de leerling] ondervindt wat de waardes van de ballen zijn, waardoor hij het hangmobiel in balans kan houden.’ Hierbij ligt de focus dus op het vinden van de waarden van de onbekenden. Jons geeft zijn bijlesleerling de opdracht om de hangmobiel in balans te houden met achtereenvolgens 2 tot en met 15 ballen. Ook Ietje formuleert een lesdoel rondom het oplossen van een vergelijking. Zij laat echter in het midden wat ze precies bedoelt met het oplossen van een vergelijking, en formuleert: ‘aan het einde van de les kunnen de leerlingen een eenvoudige vergelijking oplossen’. Ietje geeft haar leerlingen een werkblad met een aantal opdrachten mee, zoals ‘hoeveel witte zakjes zijn even zwaar als één zwart zakje?’ en ‘we noemen de witte zakjes nu W (van wit), de zwarte zakjes Z (van zwart) en de rode zakjes R (van rood). Beantwoord de volgende vragen: 3R = ……. W; 2Z = ……. W.’

Anna heeft als een van haar lesdoelen: ‘de student is in staat om de verhoudingen van de drie verschillende gewichten van de hangmobiel te ontdekken.’ Zij legt dus de nadruk op het ontdekken van de verhouding tussen de onbekenden en niet per se het ontdekken van de waarde van één onbekende. Haar andere lesdoelen formuleert ze als volgt ‘de student is in staat in te zien hoe je de stap van woorden naar letters kunt maken om zo te kunnen gaan letter-rekenen’ en ‘de student is in staat van de hangmobiel (informeel/concreet) naar tekenen op het bord te gaan (concreet/abstract).’ Hierin is duidelijk terug te zien dat een belangrijk lesdoel van haar was om van informeel gerepresenteerde vergelijkingen (de hangmobiel, woorden) naar formeel gerepresenteerde vergelijkingen toe te werken. Anna geeft haar mbo-studenten de opdracht om met de hangmobiel formele vergelijkingen te simplificeren. Zo geeft ze studenten de vergelijking 2Z + 3W + 2R = 3Z + 3W + 2R, waarbij het doel is dat ze gelijke onbekenden aan beide kanten weghalen (isoleren) en zo komen tot 1Z = 1R + 1W (afbeelding 2).

 

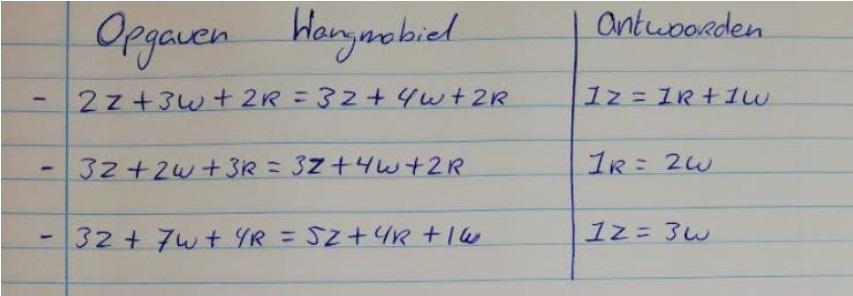
Ten slotte hadden twee leraren-in-opleiding een lesdoel rondom het exploreren van strategieën om de gelijkheid in een vergelijking te behouden. Lianne formuleerde het lesdoel ‘het uitlokken van het algebraïsch redeneren bij de leerlingen: de leerlingen zijn onbewust bezig met herstructurering, isolatie en substitutie.’ Ze gaf haar leerlingen hierbij de opdracht om te kijken wat ze allemaal kunnen veranderen aan de hangmobiel terwijl ze zorgen dat deze recht blijft. Leerlingen mochten een poster maken van alles wat ze ontdekten. Rick had als lesdoel voor zijn leerlingen ‘oefenen met de hangmobiel, kennismaken met verschillende vaardigheden die met de balansmethode (vergelijkingen) te maken hebben, algebraïsche vaardigheden.’ In tegenstelling tot de volledig open opdracht van Lianne gaf hij zijn leerlingen een gestructureerd werkblad met opdrachten als ‘maak de volgende opstelling en verwissel alle zakjes van plaats zonder ze van kant te veranderen’ gevolgd door ‘is de hangmobiel nog steeds in balans?’ of ‘haal drie zakjes weg zonder de balans te verstoren.’

 

Er zijn drie categorieën te herkennen in de door de leraren-in-opleiding geformuleerde lesdoelen:

1. Het oplossen van vergelijkingen (Ietje, Anna, Jons)
2. De overgang van een informele naar een formele representatie van een vergelijking (Anna)
3. Het exploreren van strategieën om de gelijkheid in een vergelijking te behouden (Lianne, Rick)

Bovenstaande tezamen genomen valt op dat drie leraren-in-opleiding in hun vraagstelling behoorlijk snel toewerken naar opgaven met formele vergelijkingen. Dit zijn de leraren-in-opleiding die dat expliciet in hun lesdoel verwerkt hebben (Anna), maar ook leraren-in-opleiding die de focus leggen op het oplossen van vergelijkingen (Jons en Ietje). Dit gaat beduidend sneller dan in de beschrijving van de activiteit is meegegeven, echter vertoont het wel overeenkomsten met hoe het in de les op de opleiding is geïntroduceerd. De leraren-in-opleiding geven eerst zelf uitleg waar een bepaalde formele notatie voor staat, waarna hun leerlingen zelf formeel gerepresenteerde vergelijkingen moeten oplossen. Opvallend hierbij is dat verschillende leraren-in-opleiding hun leerlingen uitleggen dat ‘W’ staat voor ‘wit’, in plaats van voor het correctere ‘gewicht van het witte zakje’. Dit wordt ook wel de letter as object misconceptie genoemd (Stacey & MacGregor, 1997), waarbij letters in een vergelijking gezien worden als (representaties van) objecten in plaats van als symbool voor een aantal of hoeveelheid objecten. Een klassiek voorbeeld waarin duidelijk wordt hoe dit misgaat is het opstellen van een vergelijking voor het aantal studenten per professor, waarbij er zes keer zoveel studenten als professoren zijn (Clement et al., 1981). Veel mensen kiezen dan voor de vergelijking 6 x S_studenten = P_professor, terwijl het natuurlijk gaat om 6 x P_aantal professoren = S_aantal studenten.

Bij de lesopbouw van de overige twee leraren-in-opleiding (Lianne en Rick), die een lesdoel hadden rondom het exploreren van strategieën om de gelijkheid in een vergelijking te behouden, komt deze formele notatie minder naar voren. Bij Rick komt dit helemaal niet terug in de vraagstelling en bij Lianne kunnen leraren-in-opleiding zelf hun bevindingen representeren op een poster en zijn ze dus vrij om voor elke representatie te kiezen. Daarnaast valt het op dat de lessen van Rick en Lianne een behoorlijk onderzoekend karakter hebben, waarbij leerlingen het model uitgebreid kunnen exploreren. Hieronder zoomen we in op het lesverloop en hun eigen reflectie van twee leraren-in-opleiding.

 

Twee leraren-in-opleiding extra uitgelicht: Hoe was het lesverloop en hun reflectie daarop?

De eerste leraar-in-opleiding die we uitlichten is Anna. Zoals hierboven beschreven formuleerde Anna lesdoelen rondom het vinden van de verhoudingen tussen balletjes en rondom de overgang van het model naar de formele vergelijkingen. Anna start haar les aan haar mbo-studenten met de vraag wie van hen al bekend is met algebra. Vervolgens introduceert ze het model, door te benoemen dat dit een hangmobiel is waarmee je kan kennismaken met de ‘balansmethode van wiskunde.’ Studenten wordt gevraagd of ze weten wat dat betekent. Een student geeft antwoord: ‘als je iets aan de ene kant doet dan moet je dat ook aan de andere kant doen, dan is er weer balans.’ Anna complimenteert de student. Ze licht vervolgens toe dat de verschillende balletjes verschillende gewichten hebben, waardoor ze zich onderling anders tot elkaar verhouden. Een student vraagt: ‘Ik verstond u niet goed, zijn de witte balletjes nou het lichtste of het zwaarst?’ Anna reageert: ‘Dat mogen jullie zelf gaan ontdekken!’, waarna studenten de opdracht krijgen om met de hangmobiel te experimenteren en de verhoudingen tussen de kleuren balletjes te ontdekken. Anna merkt dat studenten een beetje vastlopen en neemt al vrij snel de regie over door de informele vergelijkingen die gerepresenteerd zijn op de hangmobiel als formele vergelijkingen op het bord te zetten. Hierbij kort ze de kleur van de balletjes af met letters. Ze noteert vergelijkingen op het bord als 3Z + 7W + 4R = 5Z + 4R + 1W en vraagt de studenten welke verhouding ze hieruit kunnen afleiden. De studenten lopen hierop vast. Anna geeft uitleg: ‘als ik hier [linkerkant van de vergelijking] iets afhaal van kan ik dat daar [rechterkant van de vergelijking] ook doen. Dat noemen ze isoleren.’ Door dezelfde factoren aan beide kanten weg te strepen laat ze zien dat 1Z = 3W. Dit doet ze bij een aantal verschillende vergelijkingen. Studenten geven aan wat verward te zijn en de uitleg niet goed te kunnen volgen.

In haar eigen reflectie op de les geeft Anna aan dat ze de les wat moeizaam vond gaan. Ze benoemt dat ze niet zo goed wist welke opdracht ze de studenten met de hangmobiel wilde laten doen. Daarom had ze maar een aantal opdrachten waar de studenten van de minor zelf de bijeenkomst ervoor aan de slag mee waren gegaan als uitgangspunt gebruikt. Ze geeft aan in haar reflectie ‘Als ik nu terug kijk ben ik te snel naar het formele niveau gegaan. Ik had liever langer op het informele niveau willen blijven.’. Doordat studenten niet op gang kwamen wilde Anna ondersteuning bieden. Ze koos ervoor om dit op het schoolbord te doen, waar het formeel representeren gemakkelijker is dan het model natekenen met verschillende kleuren.

De tweede leraar-in-opleiding die we extra uitlichten is Lianne. Het lesdoel van Lianne was het uitlokken van algebraïsch redeneren bij de leerlingen waarbij ze onbewust met strategieën als herstructureren, isolatie en substitutie bezig zijn. Ze geeft hierbij aan dat het belangrijk is dat het echt uit de leerlingen zelf komt en dat ze de opdracht spelenderwijs wil aanvliegen. Bij de introductie van de opdracht vertelt Lianne dat de hangmobiel die voor de klas hangt een soort weegschaal is. Leerlingen mogen eerst ervaren hoe de hangmobiel werkt. Ze mogen dus zelf balletjes aan de hangmobiel hangen om te kijken wat er gebeurt. Vervolgens krijgen ze de opdracht om te zorgen dat de hangmobiel in evenwicht hangt. Daarna krijgen ze de opdracht om te zorgen dat de hangmobiel recht blijft, terwijl ze wel wat mogen veranderen. Dit doen ze klassikaal. Ze mogen eerst alleen dezelfde balletjes gebruiken en daarna ook andere balletjes erbij hangen of eraf halen. Lianne vraagt aan de leerlingen om een poster te maken allerlei hangmobielen waarvan ze weten dat deze recht zijn. Leerlingen maken gebruik van verschillende notaties. Leerlingen maken tekeningen (afbeelding 3) of schrijven bijvoorbeeld op: ‘3 rode en 2 witte’, ‘wit rood rood wit rood [onder elkaar]’, of ‘8 witte = 4 rode -> ja dus weer 1 rode is 2 witte’.

 

Daarnaast gebruiken leerlingen verschillende bewoordingen wanneer ze spreken over het in balans zijn van de hangmobiel. Oftewel, ze gebruiken verschillende bewoordingen om de ‘gelijkheid’ in een vergelijking aan de duiden, bijvoorbeeld ‘twee witte staan gelijk aan één rode’, ‘twee rode zijn even zwaar als één rode en één witte’, of ‘dan is het hetzelfde’. Tijdens het werken aan de opdracht loopt Lianne rond en spoort leerlingen vooral aan om zelf te verkennen door opmerkingen als ‘probeer het maar’. Bij de nabespreking in de klas maakt Lianne een overzicht van alle mogelijke manieren waarop de klas hun bevindingen op de poster heeft opgeschreven (afbeelding 4).

 

In haar reflectie geeft Lianne aan dat ze het erg leuk vond om deze les te geven. Leerlingen waren ‘super enthousiast’ en gebruikten direct vanaf de eerste keer dat ze balletjes aan de hangmobiel hingen woorden als ‘is gelijk aan’. Dat vond ze erg leuk om te zien. Ze gaf aan dat ze het normaal wel lastig vindt om een ‘vrije les’ te geven, maar dat het deze keer heel goed ging en dat leerlingen tijdens het werken met de hangmobiel onbewust bezig waren met algebraïsche strategieën.

 

Duiding

Anna benadrukt vanaf het begin dat ze aan de slag gaan met ‘algebra’ en met de ‘balansmethode van wiskunde.’ Tegelijkertijd doet ze haar best om studenten het model zelf te laten exploreren door onderzoekende vragen te stellen. Vanaf de start probeert ze studenten zelf dingen te laten ontdekken. Dit blijkt uit opmerkingen als ‘je gaat zo zelf ontdekken welk balletje het lichtst is’ en ‘ga maar proberen of het uitmaakt hoe hoog je het balletje ophangt.’ De opdracht van het vinden van de verhoudingen is vanaf het begin echter al redelijk sturend. Studenten begrijpen deze opdracht niet volledig en komen hierdoor onvoldoende op gang. Anna merkt dit en probeert leerlingen mee te krijgen door het oplossen van formele vergelijkingen op het bord voor te doen. Hierbij gebruikt ze zelf letters in plaats van dat ze bijvoorbeeld balletjes kleurt of de balletjes uitschrijft (afbeelding 2). Ze laat de hangmobiel – de informele vergelijking – dus al vrij snel los en maakt ook geen gebruik van de fysieke hangmobiel die aanwezig is in het lokaal. Bij de uitleg op het bord gaat ze vrij snel een strategie (isoleren) uitleggen, in plaats van dat de studenten die zelf ontdekken en ervaren. Omdat deze uitleg ook nog eens bij volledig formele vergelijkingen plaatsvindt is het voor studenten lastig te volgen wat ze aan het doen is. De in het ontwerp bedoelde toegevoegde waarde van de hangmobiel, namelijk het ontdekken in de informele context, verdwijnt hiermee volledig. De reflectie van Anna hierop is erg sterk. Ze erkent dat ze te snel naar de formele vergelijkingen heeft toegewerkt. Ze gaf aan dat haar doel was om deze formele vergelijkingen door studenten na te laten maken op de hangmobiel om vervolgens deze vergelijkingen ‘handelend op te laten lossen.’

Lianne formuleert een zeer open opdracht met de hangmobiel. Het is duidelijk dat de leerlingen op een informele manier bezig zijn met algebraïsche strategieën. Daarnaast maakt Lianne in de nabespreking de eerste stap naar het ontwikkelen van formele notaties. Hierbij is het sterk dat ze notaties van de leerlingen als uitgangspunt neemt. Opvallend is dat zij de enige student is die vrijwel volledig de opzet en uitvoering van de les met de hangmobiel heeft gevolgd zoals die in het oorspronkelijke onderzoek is gedaan (Otten et al., 2019). Hierdoor is het open karakter, de focus op informele en concreet handelen en de onderzoekende focus in haar les sterk vertegenwoordigd, precies zoals de bedoeling van de ontwerpers van de activiteit was.

 

Conclusie en discussie

Uit de beschrijving van de lesdoelen en illustraties vanuit de lessen van vijf leraren-in-opleiding en de uitgebreide beschrijving van lesverloop en lesreflectie van Anna en Lianne komt een gemengd beeld naar voren. In de oorspronkelijke opzet van de activiteiten met de hangmobiel en de les op de opleiding stonden de kernelementen van het mathematiseren van de relaties tussen de balletjes op de hangmobiel, het open en daardoor onderzoekende karakter van de vragen en activiteiten, en de belichaamde/fysieke ervaring van het uitvoeren van de algebraïsche strategieën met de balletjes op de hangmobiel centraal. Leraren-in-opleiding bleken veelal aanpakken te willen uitleggen, waardoor het zelf ervaren, het open en het onderzoekende van de activiteit met de hangmobiel teniet worden gedaan. Ook laten de leraren-in-opleiding de hangmobiel als informeel en concreet model van een vergelijking snel varen en schrijven formele vergelijkingen op het bord. Daarmee slaan ze stappen over in het mathematiseren en springen meteen van informeel naar formeel. Mogelijk heeft de snelle overgang richting de formele algebra te maken met het beeld wat deze leraren-in-opleiding hebben van algebra, namelijk ‘rekenen met letters’. Door algebra puur te zien als het uitvoeren van bewerkingen met letters, wordt het redeneren wat hieraan ten grondslag ligt minder op waarde geschat. Juist de informele contexten waarin sprake is van een vorm van gelijkheid – denk aan een balansmodel, maar ook bijvoorbeeld aan een touwtreksituatie (zie bijvoorbeeld Kindt et al., 1998) – zijn bij uitstek geschikt voor het uitlokken van dit redeneren. Alleen Lianne voert de stappen van het mathematiseren wel zo uit en ervaart ook de successen hiervan (‘erg leuk’ en ‘super enthousiast’). Opvallend en hoopgevend richting de toekomst is dat de leraren-in-opleiding erg sterk waren in hun reflecties op hun handelen en onderliggende keuzes, waardoor ze wellicht een volgende keer meer aandacht aan het informele handelen zullen besteden. Voor de lerarenopleiding blijft het een punt van aandacht om het belang van het concrete informele handelen als basis van formeler reken-wiskundig redeneren voldoende te blijven benadrukken.

In eerder onderzoek kwam naar voren hoe het algebraïsch redeneren van leerlingen in de bovenbouw van het primair onderwijs zich ontwikkelde bij het werken met de hangmobiel. Nu is het door deze leraren-in-opleiding ook beproefd in het voortgezet onderwijs en het middelbaar beroepsonderwijs, waarbij hun leerlingen of studenten goed uit de voeten leken te kunnen met de materie. Dat een dergelijke opbouw voor het ontwikkelen van algebraïsch redeneren post kan vatten in verschillende onderwijssectoren is met het oog op doorlopende leerlijnen van wiskundige concepten en activiteiten een geruststellende bevinding.