Oogbewegingsonderzoek naar diagrammen. Pleidooi voor gebruik van stippendiagrammen op de basisschool
Dit artikel bepleit de introductie van stippendiagrammen en varianten daarvan, zoals histodots en hoeddiagrammen, in het basisonderwijs om de overgang van casus-staafdiagrammen naar histogrammen en boxplots te ondersteunen en om hardnekkige misvattingen te verminderen. Het nieuwe kerndoel data voor rekenen-wiskunde legt de nadruk op gegevens verzamelen, analyseren en interpreteren. Hoewel diagrammen essentieel zijn voor data-analyse en -interpretatie, komen stippendiagrammen, die internationaal veel worden gebruikt, nauwelijks voor in Nederlandse schoolboeken.
Oogbewegingsonderzoek onder 50 middelbare scholieren liet zien dat casus-staafdiagrammen en histogrammen vaak worden verward, wat leidt tot ongeschikte strategieën. De gebruikte stippendiagrammen, die alle data tonen, stimuleren daarentegen effectieve strategieën, zoals het zoeken naar evenwichtspunten voor het schatten van gemiddelden in een histogram.
Ik beschrijf voorbeelden uit internationaal onderzoek die laten zien hoe stippendiagrammen en varianten daarvan, zoals hoeddiagrammen, effectief kunnen worden toegepast in het basisonderwijs. Deze voorbeelden illustreren dat statistisch redeneren vanaf jonge leeftijd al kan worden bevorderd en bieden inspiratie voor de integratie ervan in de Nederlandse onderwijspraktijk.
Het nieuwe kerndoel data
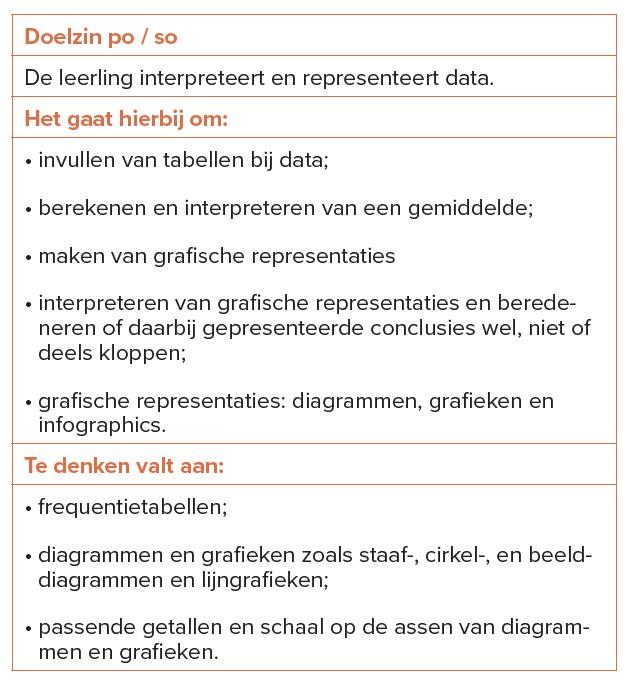
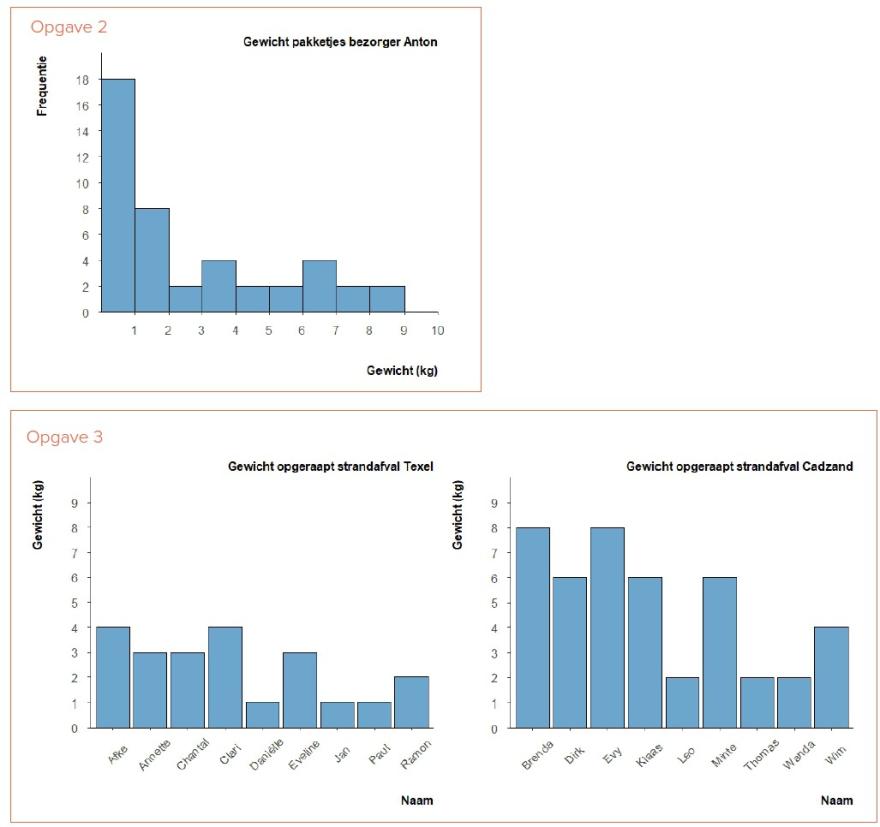
In Nederland krijgt ‘data’ een steeds belangrijke rol in het primair onderwijs zoals blijkt uit kerndoel 5 (tabel in afbeelding 1): het interpreteren en representeren van data. Spelenderwijs verzamelen leerlingen ook nu al data, bijvoorbeeld door vragen over huisdieren of lengte van leerlingen. Diagrammen zijn belangrijk voor de analyse en interpretatie van data. Basisscholen gebruiken regelmatig casus-staafdiagrammen (Boels, 2019a) voor kwantitatieve meetwaarden. Hierbij staat elke staaf voor één meting en geeft de hoogte de gemeten waarde weer (afbeelding 2). In het voortgezet onderwijs (vo) leren leerlingen histogrammen (en boxplots) te interpreteren. In histogrammen geeft de breedte van de staaf een klasse van meetwaarden weer en geeft de staafhoogte het aantal meetwaarden in die klasse (afbeelding 3). Hoewel deze diagrammen visueel op elkaar lijken (zie ook afbeelding 5), moeten ze anders worden geïnterpreteerd. Dit artikel bespreekt de problemen bij het interpreteren van histogrammen, met voorbeelden uit oogbewegingsonderzoek, en biedt een oplossing gebaseerd op internationaal onderzoek (Fielding-Wells, 2018; Frischemeier, 2023) en curricula (Bargagliotti et al., 2020; CCSS, n.d.): stippendiagrammen en varianten daarop als tussenstap in het primair onderwijs (afbeelding 4). In kaders geef ik ter inspiratie enkele voorbeelden voor het primair onderwijs.
Diagrammen met één statistische variabele en interval- of ratio meetniveau
Dit artikel richt zich op diagrammen van één variabele die op interval- of ratio meetniveau[i] gemeten is; met uitzondering van casus-staafdiagrammen vanwege hun visuele gelijkenis met histogrammen. Cirkel-, lijn- en spreidingsdiagrammen worden buiten beschouwing gelaten, omdat deze respectievelijk nominaal meetniveau of twee statistische variabelen vereisen. Steel-bladdiagrammen worden niet behandeld vanwege het beperkte onderzoek hierover (Boels, 2025) en hun zeldzaamheid in praktijk en literatuur. Een enkel praktijkvoorbeeld is de bustabel (Boels et al., 2022). Dichtheidshistogrammen en frequentiepolygonen, als logisch vervolg op histogrammen in vo, blijven eveneens buiten beschouwing.



Het probleem
Casus-staafdiagrammen (afbeelding 2) en histogrammen (afbeelding 3) worden regelmatig verward door leerlingen, door studenten in het hbo/wo en door docenten (Cooper & Shore, 2008; Boels, et al., 2018, 2024; Boels, Bakker, Van Dooren, et al., 2019). Deze problemen zijn al decennia bekend (e.g., Ismail & Chan, 2015; Pettibone & Diamond, 1972). Analyses van leerlingproblemen, gebaseerd op hun antwoorden (Whitaker et al., 2015) en zorgvuldig uitgevoerde interventies (onder andere Kaplan et al., 2014) hebben deze verwarring niet verminderd. Dat maakte een gedetailleerdere analyse noodzakelijk.
Om beter te begrijpen, welke strategieën leerlingen gebruiken om tot hun antwoord te komen, is een oogbewegingsonderzoek uitgevoerd met 50 leerlingen uit de bovenbouw van het vwo (Boels et al., 2024), omdat histogrammen doorgaans pas dan zijn geleerd. In het onderzoek zijn daarnaast casus-staafdiagrammen en de internationaal in het primair onderwijs vaker gebruikte stippendiagrammen meegenomen (bijvoorbeeld CCSS, n.d.).
Het voordeel van een oogbewegingsonderzoek ten opzichte van hardop-denken, is dat oogbewegingsonderzoek details van het kijkgedrag van leerlingen laten zien waarvan leerlingen zich vaak niet bewust zijn. Hardop denken is een minder geschikte onderzoeksmethode, omdat het de aanpak en oogbewegingen van leerlingen beïnvloedt (Van Gog et al., 2005).
In het onderzoek kregen leerlingen 25 opgaven met casus-staafdiagrammen, ‘gewone’ en horizontale histogrammen, en ‘rommelige’ en gestapelde stippendiagrammen. Ze schatten het gemiddelde gewicht van de data in één diagram of vergeleken dit tussen twee diagrammen van hetzelfde type (afbeelding 5). In dat laatste geval werd gevraagd voor welk diagram het gemiddelde gewicht hoger was: links, rechts of beide (ongeveer) gelijk. In interviews achteraf lieten we de helft van de leerlingen hun oogbewegingen terugzien en vroegen we hen hun aanpak te beschrijven om de oogbewegingspatronen te kunnen koppelen aan strategieën.
Twee strategieën voor het schatten van het gemiddelde domineerden. Bij de eerste zoeken deelnemers[ii] het balans- of evenwichtspunt van het diagram (waarbij een denkbeeldige verticale lijn kan worden getrokken, afbeelding 6, boven). Een leerling (L01) illustreert dit bij opgave 2 (afbeelding 5, links):
‘Ja, eigenlijk op dezelfde manier [als in de vorige opgave; dat was ook een histogram] de… degene met de hoogste piek, het meeste meewegen. En hier is eigenlijk één grote piek dus je neemt... . Ik nam ongeveer het midden en dan een beetje naar nul toe van het midden omdat de piek dichter bij de nul zit (gegeven antwoord: 3).’
Het woordje meewegen verwijst impliciet naar het balanspunt. Bij de tweede strategie maken deelnemers alle staven even lang (een denkbeeldige horizontale lijn, afbeelding 6, onder). Een leerling (L03) vertelde over deze tweede strategie (afbeelding 7[iii], links):
‘Kijken hoe hoog de tabellen [staven] in de grafiek zijn. En dan weer een beetje het midden er uit kiezen omdat ze, er staan er vier laag en vier een beetje hoger. Dus dan is het gemiddelde logisch [?] als het in het midden van de hoogste tabel [staaf] is.’
Deze leerling antwoordde vijf, terwijl het juiste antwoord tussen 2,6 en 4,8 lag. Hoewel de strategie hier correct is, werden gemiddelden soms overschat en leidde afronding op hele getallen tot uitkomsten buiten de antwoordmarge. Deze strategie werd regelmatig ook onterecht op histogrammen toegepast (afbeelding 7, rechts).
Ongeveer de helft van de leerlingen gebruikt voor een enkel histogram een strategie die alleen geschikt is voor een casus-staafdiagram. Het omgekeerde kwam zelden voor; in die gevallen leidde het kijkpatroon niet tot een getal maar tot een naam, waarna de deelnemer overstapte op een andere strategie (afbeelding 6, rechtsboven).
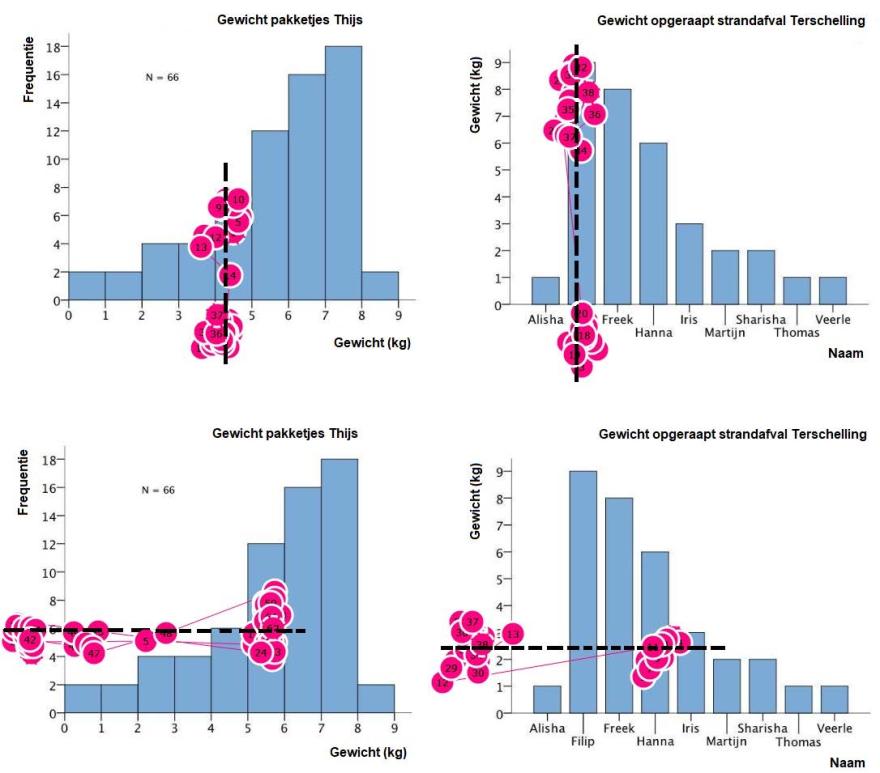
Afbeelding 6. Een deel van de oogbewegingen van leerlingen waarin hun kijkgedrag richting het antwoord goed zichtbaar is bij de taak om het gemiddelde gewicht te schatten. Het bovenste kijkgedrag hoort bij een correcte aanpak voor een histogram (linksboven); het onderste kijkgedrag hoort bij een correcte aanpak voor een casus-staafdiagram (rechtsonder).

Afbeelding 7. Deel van de oogbewegingen op een casus-staafdiagram van leerling (L03) vlak voor het geven van het antwoord vijf (links; correcte antwoord 2,6–4,8) en op een histogram van een vo-docent (D06) vlak voor het geven van het antwoord acht (correcte antwoord: 2,2–4,4)[i]
Kijkpatronen en interviews lieten zien dat leerlingen vaak denken dat elke staaf in een histogram één meetwaarde is en de hoogte de gemeten waarde. Ze begrijpen dus niet hoe data in een histogram worden weergegeven. Bij casus-staafdiagrammen klopt de interpretatie dat elke staaf één meting weergeeft en de hoogte de gemeten waarde, en is het correct om alle staven even lang te maken om het gemiddelde van de meetwaarden te vinden. In het kijkpatroon is dit terug te zien als een horizontale lijn (afbeelding 6, onder). Bij een histogram is het gemiddelde echter te vinden langs de horizontale as en moet er rekening gehouden worden met het aantal meetwaarden (de hoogte van de staven). Leerlingen kijken heen en weer tussen de gemeten waarden op de horizontale as en de top van de staaf (afbeelding 6, linksboven); soms volgt dan nog een kleine correctie naar links of rechts.
Bij het vergelijken van gemiddelden uit twee diagrammen gebruikten deelnemers specifieke kenmerken van de verdeling zoals vorm, extra of ontbrekende staven en symmetrie. Deels vergelijkbare strategieën werden gevonden in Duits onderzoek met groep 8-leerlingen (gemiddelde leeftijd 11,6 jaar) die twee onder elkaar gelegen stippendiagrammen vergeleken (Schreiter & Vogel, 2023).
Een oplossing: stippendiagrammen en varianten daarvan (histodot, hoeddiagram)
Tijdens mijn promotieonderzoek bleek dat er krachtige diagrammen zijn die de overgang van casus-staafdiagram naar histogram vergemakkelijken: stippendiagrammen (Boels, 2022) en varianten daarvan (zoals de histodot, Boels, 2019b, 2023). Stippendiagrammen tonen alle data, waarbij de positie van de stip op de getallenlijn (de horizontale as) de meetwaarde weergeeft—net als bij histogrammen.
In landen zoals Duitsland, Australië en de VS worden stippendiagrammen al in het primair onderwijs gebruikt (bijvoorbeeld Bargagliotti et al., 2020) maar in Nederlandse schoolboeken zijn ze zeldzaam; ook in het vo. In mijn oogbewegingsonderzoek naar de interpretatie van histogrammen bracht ik kijkpatronen in kaart bij twaalf taken met histogrammen en casus-staafdiagrammen. Deze taken werden gevolgd door zes ‘rommelige’ stippendiagrammen (zonder verdere uitleg) en drie histogramtaken. Vanaf het tweede stippendiagram gebruikten bijna alle leerlingen een goede strategie voor het gemiddelde (zoals het evenwichtspunt; Boels & Van Dooren, 2023). Hoewel zes taken zonder begeleiding te weinig zijn voor harde conclusies, suggereren andere studies dat stippendiagrammen effectief zijn en al in het primair onderwijs kunnen worden ingezet (Bakker, 2004; Fielding-Wells & Hillman, 2018; Frischemeier, 2023).

Ons oogbewegingsonderzoek was géén les. In een vervolgonderzoek met enkele vo-leerlingen is gekeken hoe de overgang van een stippendiagram naar een histogram kan worden gemaakt, via de histodot—een stippendiagram (‘dotplot’ in het Engels) met daaroverheen een histogram (afbeelding 9). Via digitale feedback ontdekten leerlingen zelf de juiste hoogte en betekenis van de staven. Details van deze aanpak vallen buiten dit artikel (zie Boels, 2023).

Het oogbewegingsonderzoek laat zien dat deelnemers vaak niet begrijpen hoe en waar data in een histogram worden weergegeven. In stippendiagrammen blijven alle data zichtbaar, terwijl de positie van de stip op de getallenlijn, net als in histogrammen en boxplots, de meetwaarde weergeeft. Mijn en ander onderzoek (Bakker, 2004; Boels, 2023; Fielding-Wells, 2018; Frischemeier, 2023) suggereren dat stippendiagrammen en varianten ervan zoals de histodots en hoeddiagrammen een ontbrekende schakel vormen tussen casus-staafdiagrammen en histogrammen of boxplots (zie ook afbeelding 4 en Boels, 2025).
De voorbeelden in de kaders laten zien dat stippendiagrammen al in het basisonderwijs kunnen worden gebruikt. Op basis van mijn oogbewegingsonderzoek en Duits onderzoek (Boels, 2023; Schreiter & Vogel, 2023) adviseer ik rommelige stippendiagrammen (afbeelding 8 en 12) boven netjes gestapelde (afbeelding 10 en 11), omdat die laatste vaak dezelfde verkeerde strategieën oproepen als histogrammen. Hoewel internationale studies aantonen dat stippendiagrammen effectief zijn, is er in Nederland weinig onderzoek naar gedaan (zie Van Galen & Van Eerde, 2017). Vertaling en aanpassing naar de Nederlandse situatie is nodig. Geïnteresseerde scholen kunnen contact opnemen voor samenwerking.
Van casus-staafdiagrammen naar stippendiagrammen
Het casus-staafdiagram en stippendiagram worden in sommige landen al in het primair onderwijs gebruikt. In Duitsland hielden leerlingen van 10–11 jaar (groep 7) hun reistijd naar school bij, eerst op papier en later digitaal (afbeelding 10 en 11; Frischemeier, 2023). Ze redeneerden daarbij over individuele en groepen leerlingen (modale klomp: de meeste leerlingen zitten tussen … en … minuten). Het gebruik van een horizontaal casus-staafdiagram (afbeelding 11, boven) biedt didactische voordelen, zoals dat de gemeten waarden langs de horizontale as staan (Bakker, 2004; Boels, Bakker, Van Dooren, et al., 2019).

Afbeelding 10. Aantal minuten dat leerlingen naar school gaan, leerlingenwerk (Frischemeier, 2023)
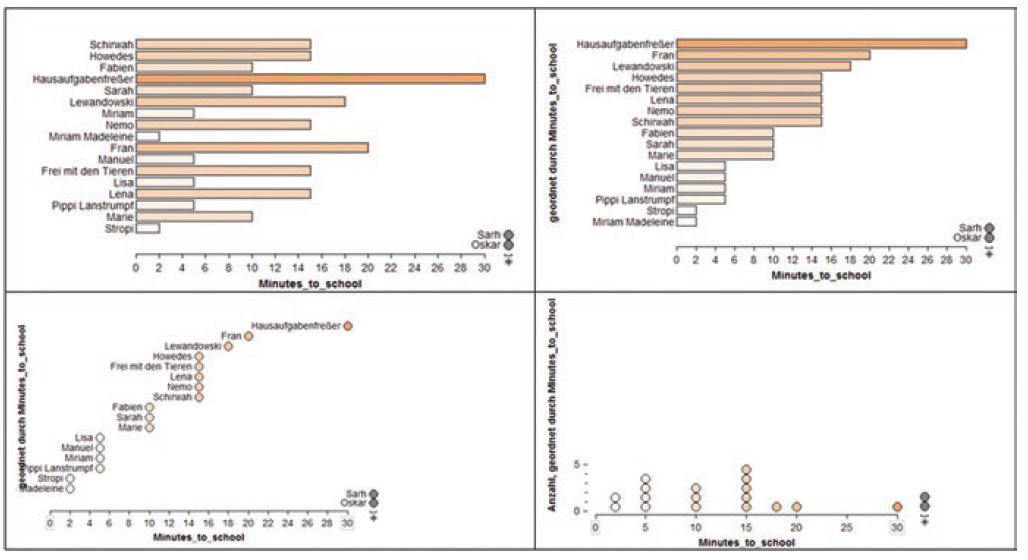
Afbeelding 11. Een casus-staafdiagram (boven) en gestapeld stippendiagram (rechtsonder) gemaakt met TinkerPlots (de opvolger hiervan, Codap, is gratis te gebruiken: https://codap.concord.org/ ). “This was done by the teacher on the board in an explain-the-screen setting (Drijvers, 2012) where the teacher discussed what the students can extract from the unordered value bars and how the representation can be improved”. (Frischemeier, 2023, p. 89)
Van stippendiagram via hoeddiagrammen op weg naar boxplots
Stippendiagrammen kunnen de overgang naar boxplots ondersteunen. In Australië vergeleken leerlingen uit groep 6 (9–10 jaar) de afstanden van papieren vliegtuigen, gemaakt van 10 x 15 cm en 20 x 30 cm papier (en later nog groter; Fielding-Wells & Hillman, 2018). De data werden weergegeven in stippendiagrammen, eerst op papier en later met software (afbeelding 12). Leerlingen bepaalden per type vliegtuig een goede maat voor de afstanden, de modale klomp genoemd. Door deze klomp over de data te tekenen, ontstond een hoeddiagram (hatplot), een voorbereiding op het leren van boxplots in het voortgezet onderwijs.
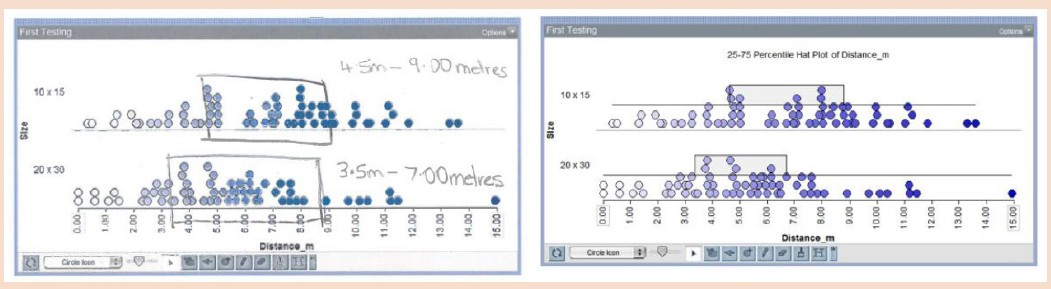
Afbeelding 12 De afstanden die een goede maat waren voor de twee typen vliegtuigen volgens Janice (links; getekend op een schermafdruk) en met de “hat” functie van TinkerPlots (rechts) (Fielding-Wells & Hillman, 2018)
[i] In Boels (2017) leg ik meetniveaus uit. Kort samengevat: nominaal meetniveau omvat bijvoorbeeld geslacht of lievelingskleur; ordinaal meetniveau bijvoorbeeld temperatuur aangeduid als koud, lauw, warm, heet; interval meetniveau bijvoorbeeld temperatuur in graden Celsius; ratio meetniveau bijvoorbeeld lengte (zie ook Drijvers & Voorhoeve, 2017).
[ii] Onderzoek onder docenten (Boels, Bakker & Drijvers, 2019) en universitaire studenten (Boels et al., 2018) gaf vergelijkbare resultaten. Daarom gebruik ik ‘deelnemers’, tenzij specifiek verwezen wordt naar de 50 leerlingen.
[iii] Hoewel dit patroon breder is omdat nu alle oogbewegingen over elkaar liggen, onder andere door het zoeken naar de specifieke waarde voor het gemiddelde, is ook hierin een verticaal kijkpatroon te herkennen (bij een horizontaal oogbewegingspatroon, liggen de stippen meer op een brede horizontale lijn). De oogbeweging naar rechtsonder (boven de knop ‘volgende’) zijn voor het kijkpatroon niet relevant. De oogbewegingen rechtsboven (nummer 1–12) zijn ontstaan doordat op het vorige scherm hier een fixatiekruis stond; het duurt dan even voordat de ogen zich fixeren op de tekst van de nieuwe opgave (linksboven). De software die gebruikt is om deze afbeeldingen te maken, draait alleen op Windows 7. Aangezien we geen laptop meer hebben die daarvoor geschikt is, is het technisch niet mogelijk om een vergelijkbare afbeelding te maken als voor de andere is gedaan. Alleen de afbeeldingen die we destijds hebben gemaakt, zijn daardoor beschikbaar.
The article advocates the inclusion of dotplots and variants thereof (histodots, hatplots) in primary education to support the transition from case-value plots to histograms and boxplots, and to address persistent misinterpretations. The new Dutch primary curriculum emphasises data collection, analysis and interpretation. Although graphs are essential for data analysis and interpretation, dotplots and their variants, which are widely used internationally, are hardly included in Dutch text books.
Eye-tracking research among 50 secondary school students revealed confusion between case-value plots and histograms, resulting in strategies inappropriate for histogram tasks. While students often misinterpret bars in histograms as individual data points, dotplots—which show all data values—encourage correct strategies such as searching histograms’ balancing points to estimate means.
The article includes examples from international research showing how dotplots and their variants, such as hatplots, can be used effectively in primary education. These examples highlight the possibilities of promoting statistical reasoning from an early age and offer inspiration for its integration into Dutch educational practice.
[i] In Boels (2017) leg ik meetniveaus uit. Kort samengevat: nominaal meetniveau omvat bijvoorbeeld geslacht of lievelingskleur; ordinaal meetniveau bijvoorbeeld temperatuur aangeduid als koud, lauw, warm, heet; interval meetniveau bijvoorbeeld temperatuur in graden Celsius; ratio meetniveau bijvoorbeeld lengte (zie ook Drijvers & Voorhoeve, 2017).
[i] Hoewel dit patroon breder is omdat nu alle oogbewegingen over elkaar liggen, onder andere door het zoeken naar de specifieke waarde voor het gemiddelde, is ook hierin een verticaal kijkpatroon te herkennen (bij een horizontaal oogbewegingspatroon, liggen de stippen meer op een brede horizontale lijn). De oogbeweging naar rechtsonder (boven de knop ‘volgende’) zijn voor het kijkpatroon niet relevant. De oogbewegingen rechtsboven (nummer 1–12) zijn ontstaan doordat op het vorige scherm hier een fixatiekruis stond; het duurt dan even voordat de ogen zich fixeren op de tekst van de nieuwe opgave (linksboven). De software die gebruikt is om deze afbeeldingen te maken, draait alleen op Windows 7. Aangezien we geen laptop meer hebben die daarvoor geschikt is, is het technisch niet mogelijk om een vergelijkbare afbeelding te maken als voor de andere is gedaan. Alleen de afbeeldingen die we destijds hebben gemaakt, zijn daardoor beschikbaar.
Bakker, A. (2004). Design research in statistics education. On symbolizing and computer tools. [Dissertation]. Utrecht University. https://dspace.library.uu.nl/bitstream/handle/1874/893/full.pdf
Bargagliotti, A., Franklin, C., Arnold, P., Gould, R., Johnson, S., Perez, L., & Spangler, D. (2020). Pre-K-12 guidelines for assessment and instruction in statistics education (GAISE) report II. American Statistical Association and National Council of Teachers of Mathematics. https://www.amstat.org/docs/default-source/amstat-documents/gaiseiiprek-12_full.pdf
Boels, L. (2017). Kleintje didactiek. Meetniveaus, Euclides, 93(3), 28–29. https://archief.vakbladeuclides.nl/bestanden/093_2017-18_03.pdf
Boels, L. (2019a). FIzier. Wat elke docent zou moeten weten over histogrammen, Euclides 94(4), 10–13. https://archief.vakbladeuclides.nl/bestanden/094_2018-19_04.pdf
Boels, L. (2019b). Kleintje didactiek. Histodot - een nieuw type grafiek, Euclides, 94(5), 31. https://archief.vakbladeuclides.nl/bestanden/094_2018-19_05.pdf
Boels, L. (2022). Kleintje didactiek. Interpreteren van histogrammen en stippengrafieken, Euclides, 97(5), 20.
Boels, L. (2023). Histograms. An educational eye [Dissertation]. Utrecht University. https://www.fisme.science.uu.nl/publicaties/literatuur/20230822_proefschrift_boels.pdf
Boels, L. (2025). Developing students’ understanding of statistical graphs: A local instruction theory. [Poster]. CERME14. Bozen-Bolsano, Italy.
Boels, L., Alberto, R. & Shvarts, A. (2023). Actions behind mathematical concepts: A logical-historical analysis. In P. Drijvers, C. Csapodi, H. Palmér, K. Gosztonyi, & E. Kónya (Eds.), Proceedings of the Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13) (pp. 5083–5090). Alfréd Rényi Institute of Mathematics and ERME. https://hal.science/CERME13/hal-04420753v1
Boels, L., Bakker, A., & Drijvers, P. (2019). Unravelling teachers’ strategies when interpreting histograms: an eye-tracking study. In U.T. Jankvist, M. Van den Heuvel-Panhuizen, & M. Veldhuis (Eds.), Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, (pp. 888–895). Utrecht, The Netherlands: Freudenthal Group & Freudenthal Institute, Utrecht University and ERME. https://hal.archives-ouvertes.fr/hal-02411575/document
Boels, L., Bakker, A., Van Dooren, W., & Drijvers, P. (2024). Secondary school students’ strategies when interpreting histograms and case-value plots: An eye-tracking study. Educational Studies in Mathematics. https://doi.org/10.1007/s10649-024-10351-3
Boels, L., Bakker, A., Van Dooren, W., & Drijvers, P. (2019). Conceptual difficulties when interpreting histograms: A review. Educational Research Review, 28, Article 100291, https://doi.org/10.1016/j.edurev.2019.100291
Boels, L., Ebbes, R., Bakker, A., Van Dooren, W., & Drijvers, P. (2018). Revealing conceptual difficulties when interpreting histograms: an eye-tracking study. Invited paper, refereed. In M. A. Sorto, A. White, & L. Guyot (Eds.), Looking back, looking forward. Proceedings of the Tenth International Conference on Teaching Statistics, pp. 1–4, Kyoto, Japan. Voorburg, The Netherlands: International Statistical Institute. https://iase-web.org/icots/10/proceedings/pdfs/ICOTS10_8E2.pdf
Boels, L., Hoogland, K., Jonker, V., Kleine Deters, B., & Wijers, M. (2022) Het interpreteren en begrijpen van hedendaagse informatiebronnen [Interpreting and making sense of contemporary information sources]. (pp. 1–84). HU University of Applied Sciences Utrecht.
Boels, L., & Van Dooren, W. (2023). Secondary school students interpreting and comparing dotplots: An eye-tracking study. In M. Ayalon, B. Koichu, R. Leikin, L. Rubel & M. Tabach (Eds.). Proceedings of the 46th Conference of the International Group for the Psychology of Mathematics Education, 2, (pp. 123–130). PME. Haifa, Israel. https://www.researchgate.net/publication/372448356_Secondary_school_students_interpreting_and_comparing_dotplots_An_eye-tracking_study
Common Core State Standards for Mathematics (CCSS, n.d.). Common Core State Standards Initiative. https://corestandards.org/mathematics-standards/
Cooper, L. L., & Shore, F. S. (2008). Students’ misconceptions in interpreting center and variability of data represented via histograms and stem-and-leaf plots. Journal of Statistics Education, 16(2), https://doi.org/10.1080/10691898.2008.11889559
Dunn, P. K. (2018). Babyboom [data file]. https://ww2.amstat.org/publications/jse/jse_data_archive.htm
Drijvers, P. & Voorhoeve, M. (2017). Vier meetniveaus (paragraaf 2.2). Open Online Bètadidactiek. http://maken.wikiwijs.nl/86112/Didactiek_van_statistiek
Fielding-Wells, J. (2018). Dot plots and hat plots: Supporting young students emerging understandings of distribution, center and variability through modeling. ZDM Mathematics Education 50, 1125–1138. https://doi.org/10.1007/s11858-018-0961-1
Fielding-Wells & Hillman (2018). Supporting young students emerging understandings of centre through modelling. In M. A. Sorto, A. White, & L. Guyot (Eds.), Looking back, looking forward. Proceedings of the Tenth International Conference on Teaching Statistics (ICOTS10, July, 2018), Kyoto, Japan. International Statistical Institute. https://iase-web.org/icots/10/proceedings/pdfs/ICOTS10_2B1.pdf?1531364242
Frischemeier, D. (2023). Reading and interpreting distributions of numerical data in primary school. In: Burrill, G.F., de Oliveria Souza, L., Reston, E. (eds). Research on Reasoning with Data and Statistical Thinking: International Perspectives. Advances in Mathematics Education. Springer. https://doi.org/10.1007/978-3-031-29459-4_11
Ismail, Z., & Chan, S. W. (2015). Malaysian students’ misconceptions about measures of central tendency: An error analysis. In Proceedings of the AIP Conference (pp. 93–100). AIP. https://doi.org/10.1063/1.4907430
Kaplan, J. J., Gabrosek, J. G., Curtiss P., & Malone, C. (2014). Investigating student understanding of histograms. Journal of Statistics Education, 22(2), 1–30. https://doi.org/10.1080/10691898.2014.11889701
Pettibone, T. J., & Diamond, J. J. (1972). An incorrect index of skewness. Resources in Education, 8(1–4), 1–8. https://eric.ed.gov/?id=ED068579
Schreiter, S., & Vogel, M. (2023). Eye-tracking measures as indicators for a local vs. global view of data. Frontiers in Education, 7. https://doi.org/10.3389/feduc.2022.1058150
Van Galen, F., & Van Eerde, D. (2017). Statistiek in het basisonderwijs. In M. van Zanten (red.) (2017). Rekenen-wiskunde in de 21e eeuw. Ideeën en achtergronden voor primair onderwijs (pp. 43–52). Panama, Universiteit Utrecht, NVORWO, SLO. https://www.fisme.science.uu.nl/publicaties/literatuur/2017_StatistiekInHetBasisonderwijsGalenEerde.pdf
Van Gog, T., Paas, F., Van Merriënboer, J. J., & Witte, P. (2005). Uncovering the problem- solving process: Cued retrospective reporting versus concurrent and retrospective reporting. Journal of Experimental Psychology: Applied, 11(4), 237–244. https://doi.org/10.1037/1076-898X.11.4.237
Whitaker, D., & Jacobbe, T. (2017). Students’ understanding of bar graphs and histograms: Results from the LOCUS assessments. Journal of Statistics Education, 25(2), 90–102. https://doi.org/10.1080/10691898.2017.1321974
