Hogere ambities voor beter reken-wiskundeonderwijs

Dit artikel analyseert de ontwikkeling van kerndoelen en referentieniveaus en biedt inzicht in de prestatietrends van leerlingen en scholen. Trendanalyses laten een stagnatie zien in de behaalde rekenniveaus, zowel op leerlingniveau als op schoolniveau. De meerderheid van de basisscholen slaagt er niet in om structureel het streefniveau 1S te behalen, terwijl de aansluiting tussen primair en voortgezet onderwijs een hogere ambitie vereist. Dit artikel sluit aan bij eerdere aanbevelingen van de Onderwijsraad en benadrukt vier kernaspecten: (1) het belang van duidelijke en meetbare prestatienormen voor scholen, (2) de noodzaak van gelijke kansen door een betere borging van rekenvaardigheden, (3) transparantie in schooltrends om gerichte beleidsinterventies mogelijk te maken, en (4) effectieve ondersteuning voor scholen die structureel onder de norm presteren. De bevindingen onderstrepen de noodzaak van een systematische, op data gebaseerde aanpak voor schoolverbetering. Dit vraagt om nader onderzoek naar succesvolle rekenstrategieën op scholen en de impact van didactische keuzes op leerprestaties. Zonder een hernieuwde focus op ambitie en niveaubewaking blijft structurele verbetering van het reken-wiskundeonderwijs uit.

 

De vicieuze cirkel in de ontwikkeling van kerndoelen

 

De eerste kerndoelen: veel en niet concreet genoeg

De eerste kerndoelen werden in 1993 geformuleerd om, na de invoering van de Wet op het Basisonderwijs in 1985, meer helderheid en samenhang in het onderwijsaanbod van basisscholen te creëren (Staatsblad, 1993). De kerndoelen voor rekenen-wiskunde waren destijds relatief eenvoudig op te stellen, aangezien de inhoud al grotendeels was beschreven in vijfentwintig jaar werk binnen het Wiskobas-project en de opvolging daarvan. Het Wiskobas-project legde vanaf 1971 de basis voor wat later bekend werd als realistisch rekenen. Met de ‘Proeve publicaties’ werd het gedachtegoed van realistisch rekenen in Nederland een eensgezinde aanpak en verheven tot de grondslag voor een nationaal programma voor het reken-wiskundeonderwijs (Treffers et al., 1989). De eerste kerndoelen voor rekenen-wiskunde worden ook wel gezien als het sluitstuk van dat ontwikkelexperiment (Commissie Kerndoelen, 2002).

 

Tweede kerndoelen: concreter, met tussendoelen

Kort na de formalisering van de eerste kerndoelen werd de commissie ‘Heroverweging kerndoelen’ ingesteld omdat de kerndoelen niet haalbaar bleken, vooral door overladenheid en de te zware organisatorische belasting van de school (Ministerie van Onderwijs, 1995). De commissie stelde voor de eerste kerndoelen opnieuw te ordenen en concreter te  beschrijven (Commissie Heroverweging Kerndoelen Basisonderwijs, 1994). Dit resulteerde in een nieuwe, concretere versie van de tweede kerndoelen in 1998 (Staatsblad, 1998).

Voor rekenen-wiskunde werd echter een andere aanpak gekozen om de kerndoelen verder te concretiseren. De kerndoelen voor rekenen-wiskunde bleven nagenoeg ongewijzigd omdat er concrete tussendoelen zouden worden opgesteld. Voor de concretisering van de kerndoelen voor rekenen-wiskunde werd het zogenaamde ‘Tussendoelen annex Leerlijnen project’ (TAL-project) gestart (Van den Heuvel-Panhuizen et al., 1998). Uit de evaluatie van het TAL-project (Van der Wel et al., 2002) blijkt echter dat leraren het materiaal moeilijk konden toepassen en zij zich afvroegen hoe je met al de verschillende doelen (kerndoelen, lvs-doelen, methodedoelen en tussendoelen) zou moeten omgaan. Volgens de evaluatie gaven leraren aan niet te weten welke doelen prioriteit hadden voor de toetsing.

 

Derde kerndoelen: minder en abstracte kerndoelen

De tweede kerndoelen zorgden voor een concreter maar overladen curriculum.  Zo constateerde de Onderwijsraad in het advies ‘Zeker weten’ (Onderwijsraad, 1999b) dat leraren aangaven het curriculum te vol en onoverzichtelijk te vinden. Voor scholen was onduidelijk welke kerndoelen cruciaal waren door de manier waarop de kerndoelen waren geformuleerd en ingedeeld. Daarom werd de Commissie Kerndoelen Basisonderwijs (‘Commissie Wijnen’) ingesteld om de derde kerndoelen te ontwikkelen en het aantal kerndoelen te reduceren (Commissie Kerndoelen, 2002). Met de derde kerndoelen zijn de eerdere 23 kerndoelen uit 1998 teruggebracht naar 11 kerndoelen die vanaf 2006 formeel van kracht werden (Staatsblad, 2005). Hiermee werd geprobeerd een nieuw evenwicht te vinden tussen kernachtige leerdoelen en voldoende ruimte voor scholen om hun onderwijs vorm te geven (Commissie Kerndoelen, 2002).

 

Vierde kerndoelen: weer concreter maar nog te veel

Nadat de derde kerndoelen kernachtig en ruim geformuleerd waren, bood dit scholen vervolgens weinig houvast waardoor opnieuw de behoefte aan concretere doelen ontstond. Waar eerdere kerndoelen door hun uitgebreidheid bijdroegen aan overladenheid, leidden de kernachtige formuleringen eveneens tot ervaren overladenheid, doordat voor leraren niet duidelijk was over wat verplicht was en wat vrijgelaten werd (SLO, 2024a). Daarom werd een herziening gestart via Curriculum.nu. Later gaf het ministerie van OCW SLO de opdracht de kerndoelen te actualiseren. Dit leidde tot een nieuwe set van 15 ‘definitieve conceptkerndoelen’ (SLO, 2024b). Deze zijn concreter beschreven doordat een toelichting is opgenomen in de vorm van ‘het gaat hierbij om’ en ‘te denken valt aan’ ter verduidelijking van het kerndoel. Maar deze kerndoelen zijn nog niet aangenomen door de Tweede Kamer, want de staatssecretaris heeft bij het aanbieden ervan al aangegeven dat deze opnieuw geredigeerd moeten worden, omdat het aantal kerndoelen te groot is (Ministerie van Onderwijs, 2024a).

Daarom heeft SLO de opdracht gekregen om het aantal kerndoelen opnieuw te verminderen en beter op elkaar af te stemmen. Tot het najaar van 2025 is er tijd om deze vermindering en afstemming door te voeren.

 

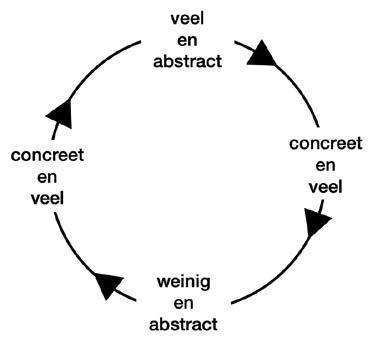
Kort samengevat laat de ontwikkeling van de kerndoelen een vicieuze cirkel zien: veel en te abstract, dan te concreet en veel, vervolgens minder en abstract, en dan concreet en veel (afbeelding 1). De ontwikkeling van de kerndoelen laat een terugkerend probleem zien: het zoeken naar balans tussen abstractie en detaillering zonder een stabiele, werkbare oplossing te vinden.

 

Naar meetbare doelen voor rekenen-wiskunde

 

De onderwijsraad: leerstandaarden voor zeker weten

De Onderwijsraad heeft vaak kritisch gestaan ten opzichte van kerndoelen vanwege het ontbreken van toetsingsmogelijkheden en duidelijke beheersingsniveaus, waardoor scholen niet weten wat leerlingen moeten bereiken (Onderwijsraad, 1997). Ondanks de reductie van kerndoelen in 2006, bleef een fundamenteel probleem bestaan: de doelen waren niet toetsbaar, wat opbrengstgericht werken bemoeilijkte (Onderwijsraad, 2002). De kerndoelen waren slechts aanbodsdoelen, terwijl er ook een streven is naar opbrengstgericht werken met meetbare doelen. Daarom adviseerde de Onderwijsraad in het eerder genoemde rapport ‘Zeker weten’ voor de invoering van zogenaamde ‘leerstandaarden’ als aanvulling op de gebruikelijke kerndoelen waarvoor slechts een inspannings- en aanbodverplichting geldt (Onderwijsraad, 1999b).

Voor basisscholen adviseerde de Onderwijsraad twee beheersingsniveaus: een minimumniveau dat door 90-95% van de leerlingen behaald zou moeten worden en een voldoende niveau voor 70-75% van de leerlingen. Deze leerstandaarden moesten concrete eisen stellen aan de kennis en vaardigheden die leerlingen op verschillende momenten in hun schoolloopbaan zouden moeten beheersen. Ook adviseerde de Onderwijsraad voor de gehele basisschool (slechts) twee meetmomenten: halverwege de basisschool in groep 4 en aan het eind in groep 8. De Onderwijsraad ging zelfs haar boekje enigszins te buiten door niet alleen te adviseren maar zelf ook een concreet voorstel uit te werken voor die leerstandaarden (Onderwijsraad, 1999a). De Onderwijsraad pleitte daarbij voor ambitieuzere leerdoelen en landelijke peilingen om het niveau te monitoren. Het streven moest zijn om de lat hoog te leggen, met niveaubewaking als noodzakelijke voorwaarde wat ook terug te zien is in de daarop volgende adviezen van de Onderwijsraad waarin het pleidooi voor leerstandaarden bijna ieder jaar wel wordt herhaald (Ledoux et al., 2009).

 

Leerstandaarden voor duidelijkheid en gelijke kansen

De Onderwijsraad legt in het adviesrapport ‘Zeker weten’ uit waarom meetbare leerstandaarden nodig zijn, met vier kernpunten die bijdragen aan een beter functionerend onderwijssysteem (Onderwijsraad, 1999b):

1. Duidelijkheid voor scholen - Leerstandaarden helpen scholen inzicht te krijgen in wat essentieel is binnen het onderwijs, zodat zij hun lespraktijk hierop kunnen afstemmen.
2. Gelijke kansen - Leerstandaarden waarborgen dat alle leerlingen toegang hebben tot dezelfde fundamentele kennis en vaardigheden.
3. Transparantie - Leerstandaarden maken het onderwijsopbrengsten inzichtelijk voor ouders, de overheid en de samenleving.
4. Gerichte ondersteuning - Leerstandaarden helpen zwak presterende scholen te identificeren, zodat zij de juiste ondersteuning kunnen krijgen om hun onderwijs te verbeteren.

Tegelijkertijd werd erkend dat meetbare leerstandaarden ook risico’s met zich meebrengen. Zo bestond de kans dat scholen zich zouden beperken tot het minimum dat getoetst werd of dat het streven naar autonomie onder druk zou komen te staan.

Het advies van de Onderwijsraad was een belangrijke stap naar ambitieus en meetbaar onderwijsbeleid, iets wat de kerndoelen niet boden. Toch duurde het nog ruim tien jaar voordat de standaarden, onder de naam ‘referentieniveaus’, daadwerkelijk werden ingevoerd.

 

Wettelijke verankering, ook leerresultaten

De geadviseerde leerstandaarden werden opgesteld door een aparte expertgroep: de ‘commissie Meijerink’ of ‘Expertgroep Doorlopende leerlijnen taal en rekenen’ (Expertgroep, 2008). Deze expertgroep gaf invulling aan de ambities door meetbare referentieniveaus te formuleren, die in basisscholen bekend werden als 1F en 2F/1S niveau. De referentieniveaus werden in 2010 wettelijk vastgelegd naast de aanbodsgerichte kerndoelen (zie Wet primair onderwijs art. 9 lid 11).

Basisscholen kregen met de referentieniveaus een instrument in handen om onderwijsresultaten beter te monitoren. Met de invoering van de verplichte eindtoets voor basisscholen rapporteerde de onderwijsinspectie er vanaf schooljaar 2014-2015 ook jaarlijks over in de Staat van het Onderwijs. Voor rekenen-wiskunde de laatste jaren ook expliciet: ‘Vooral beheersing 1S streefniveau rekenen blijft achter’ (2020, p. 58), ‘Maak van de reparatie een renovatie’ (2021, p. 5), ‘Een renovatie is urgent, de situatie is nog onveranderd zorgelijk en de verschillen tussen scholen en leerlingen zijn dit jaar verder toegenomen’ (2022, p. 5), ‘Al een aantal jaar rapporteren we dat het niveau daalt’ (2022, p. 22), ‘Het aandeel scholen waarop meer dan 65% van de leerlingen 1S beheerste was slechts 12%’ (2024, p. 42), ‘Een hernieuwde focus van het rekenonderwijs minimaal gericht op het uitstroomniveau 1S is daarom nodig’ (2024, p. 114).

Sinds 2023 laat de Inspectie van het Onderwijs de referentieniveaus ook expliciet terugkomen in het toetsingskader van basisscholen. De basisvaardigheden rekenen-wiskunde waren altijd al een aandachtspunt binnen het toezicht maar tot dan toe gericht op het onderwijsaanbod (OP1). Met de toevoeging van een aparte standaard in het onderzoekskader (OP0 Basisvaardigheden) wordt de koppeling met de wet op het primair onderwijs versterkt: voor rekenen-wiskunde is de inhoud van het curriculum ten minste dekkend voor de kerndoelen en werkt het toe naar de referentieniveaus. De referentieniveaus dienen als richtsnoer om leerlingen naar een eindniveau te begeleiden, fungeren voor het primair onderwijs als bekostigingsvoorwaarde en deugdelijkheidseis, en spelen een normerende rol in de bepaling van leerresultaten van basisscholen (Van Schoonhoven, 2023).

De invoering van de referentieniveaus betekende een belangrijke verschuiving in het monitoren, beoordelen en ondersteunen van scholen: er wordt niet alleen meer op basis van de kerndoelen naar het lesaanbod gekeken maar ook en vooral op basis van de referentieniveaus naar de leerresultaten.

 

Een effectieve doorlopende leerlijn vereist verhoogde ambities

 

Referentieniveaus voor goede aansluiting van PO naar VO

Met de invoering van de referentieniveaus voor rekenen-wiskunde zijn er voor basisscholen twee prestatieniveaus vastgelegd: het fundamentele niveau (1F) en het streefniveau (1S). De expertgroep (commissie Meijerink) kreeg de opdracht om deze duidelijke en meetbare leerstandaarden te formuleren, die moesten bijdragen aan een soepele overgang van basisonderwijs naar het voortgezet onderwijs. Hierbij is vastgelegd welke rekenvaardigheden leerlingen moeten beheersen aan het einde van de basisschool voordat zij doorstromen naar het voortgezet onderwijs. Een stabiele doorlopende leerlijn zorgt ervoor dat leerlingen met de benodigde kennis en vaardigheden en zonder achterstanden in rekenen-wiskunde in het voortgezet onderwijs instromen. De reken-wiskundekennis en -vaardigheden van het streefniveau 1S is specifiek bedoeld voor leerlingen die doorstromen naar vmbo-t, havo of vwo. En zo moeten leerlingen het 1F-niveau beheersen voordat zij naar vmbo-b-k gaan. Deze verdeling beschrijft de expertgroep ook in de oorspronkelijke publicatie: ‘de streefkwaliteit 1S is bedoeld voor leerlingen in groep 8 met rekenpotentie voor vmbo-t en havo-vwo’ (Expertgroep, 2008, p. 24). Dit werd bij de implementatie van de referentieniveaus in 2010 ook aangegeven: ‘Referentieniveau 1S omvat 1F en is het streefniveau waar de grote groep van leerlingen aan moet voldoen om een goede aansluiting te krijgen op vmbo-t of havo-vwo’ (Noteboom, 2010, p. 4). Ook in de latere evaluatie wordt dit uitgangspunt beschreven: ‘1S voor rekenen is bedoeld voor de meerderheid van de leerlingen die doorstromen naar vmbo-t of havo-vwo en het 1F-niveau is passend voor leerlingen die doorstromen naar vmbo-bb en -kb’ (Van den Broek et al., 2022, p. 38).

 

In 2008 had 65% van de leerlingen 1S nodig

Rond 2008 stroomde 65% van de leerlingen door naar vmbo-t, havo of vwo. Daarom stelde de expertgroep vast dat minstens 65% van de leerlingen het referentieniveau 1S moest behalen om een goede aansluiting op het voortgezet onderwijs te garanderen

(Expertgroep, 2008). Het percentage van 65% was daarmee een logische keuze, gebaseerd op de doorlopende leerlijn tussen het curriculum van de basisschool en dat van het voortgezet onderwijs. Uit de analyse van het reken-wiskundeniveau bleek dat destijds ongeveer 50% van de leerlingen de opgaven op 1S-niveau correct maakte. De expertgroep concludeerde dan ook dat het percentage leerlingen dat minimaal het referentieniveau 1S behaalt, zou moeten toenemen van 50% naar 65% (Expertgroep, 2008). De norm van 65% is daarmee een beleidskeuze die voortkwam uit de aansluiting tussen het curriculum van het primair en voortgezet onderwijs.

De noodzaak om het reken-wiskundeniveau te verhogen was destijds overigens al eerder vastgesteld. De ‘kwaliteitsagenda primair onderwijs’ signaleerde dat de rekenprestaties onder druk stonden en waarschuwde dat Nederland zijn traditionele voorsprong in wiskunde dreigde te verliezen (Ministerie van Onderwijs, 2007). Dit benadrukte de noodzaak van leerstandaarden en structurele verbetering van het reken-wiskundeniveau. Het ministerie van OCW beoogde dat alle scholen meer leerlingen op fundamenteel- en streefniveau brengen, en dat scholen zichzelf daarbij de vraag stellen hoe leerlingen ervoor staan en hoe dat verbeterd kan worden (Ministerie van Onderwijs, 2008).

Ook de onderwijsinspectie drong aan op een snelle invoering van deze normering gekoppeld aan referentieniveaus. De inspectie wees daarbij op onderzoeken waaruit bleek dat het niveau in vergelijking met andere landen daalde, de wiskundige geletterdheid van vijftienjarigen te wensen overliet en er een achteruitgang was op het onderdeel ‘bewerkingen’ (Inspectie van het Onderwijs, 2008). De inspectie gaf aan voorstander te zijn van referentieniveaus zodat scholen en het onderwijs op stelselniveau prestaties beter kunnen meten en vergelijken in de tijd. Daarnaast benadrukte de onderwijsinspectie dat scholen beter konden presteren door meer opbrengstgericht te werken en gerichte interventies toe te passen. Hierdoor werd de invoering van referentieniveaus niet alleen een beleidsdoel, maar ook gezien als noodzakelijke maatregel om het reken-wiskundeniveau te verbeteren.

 

Nu heeft 75% van de basisschoolleerlingen 1S-niveau nodig

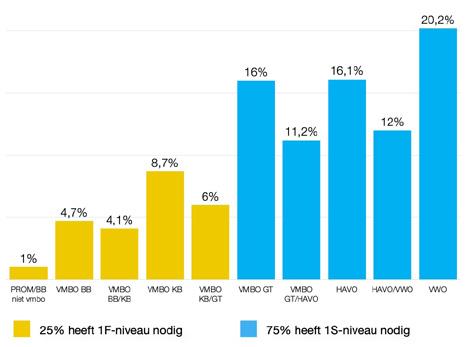
Uit de data van het huidige doorstroomadvies, blijkt dat meer basisschoolleerlingen het 1S-niveau zouden moeten beheersen aan het eind van de basisschool. Want er gaan namelijk meer leerlingen naar vmbo-g-t, havo en vwo in vergelijking met 2008 (DUO, 2024b). Dat percentage leerlingen is gestegen van 65% naar de huidige 75% (afbeelding 2). Dit maakt de noodzaak om meer leerlingen het 1S-niveau te laten beheersen alleen maar urgenter. Twee basisschoolgeneraties later zou een nieuwe expertgroep de norm verhogen van 65% naar 75% van de leerlingen die 1S moeten beheersen. In het masterplan basisvaardigheden van het ministerie van onderwijs is dat ook wat er feitelijk gebeurt. Volgens het masterplan streeft de minister ernaar dat 95% van de leerlingen minimaal 1F-niveau beheerst voor rekenen-wiskunde. Aan het einde van schooljaar 2027/2028 moet de aansluiting voor driekwart van de leerlingen op orde zijn (Ministerie van Onderwijs, 2023). Om de aansluiting op orde te hebben, moet 75% van de leerlingen aan het einde van de basisschool 1S beheersen, maar minder dan de helft van de leerlingen beheerst dat nu (46%), waardoor nog een slag te slaan is om de aansluiting met het vo op orde te krijgen (Ministerie van Onderwijs, 2024b). Waar in 2008 nog 15% van de leerlingen het benodigde niveau niet haalde, is dat nu bijna 30%, omdat meer leerlingen dit 1S-niveau tegenwoordig nodig hebben. Dit staat in contrast met wat elders wordt gesteld (Buijs, 2024), namelijk dat de norm naar beneden bijgesteld zou moeten worden omdat deze te hoog gekozen zou zijn. Er ligt een forse uitdaging: méér leerlingen zouden het 1S-niveau moeten beheersen, maar een groot deel beheerst dat niet. Niet voor niets zijn er veel extra financiële middelen beschikbaar gekomen voor de basisvaardigheden in het primair onderwijs, maar ook voor het voortgezet onderwijs (Ministerie van Onderwijs, 2022).

 

Stagnerende trend in leerlingresultaten

 

Trends bij leerlingen (groep 8)

De invoering van referentieniveaus betekende een belangrijke stap in het doorvertalen van abstracte kerndoelen naar toetsbare beheersingsniveaus. Ze vormen daarmee de basis voor zowel monitoring van leerresultaten als onderwijsbeleid om scholen ondersteuning te bieden. Om trends in de behaalde referentieniveaus en de ontwikkeling van reken-wiskundeprestaties van leerlingen in kaart te brengen, is voor dit artikel een trendanalyse van beschikbare data uitgevoerd van DUO-onderwijsdata en uit ‘De Staat van het Onderwijs’ (DUO, 2024a; Inspectie van het Onderwijs, 2024). De trendanalyse richt zich daarbij op de behaalde referentieniveaus 1S en 1F. Een statistische trendanalyse over de periode 2015-2023 wordt echter bemoeilijkt door hiaten in de beschikbare data. In 2018 ontbreken de percentages omdat de onderwijsinspectie de verschillende eindtoetsen in het primair onderwijs als onvergelijkbaar beschouwde. Daarnaast ontbreken gegevens over 2020 en 2021 vanwege de impact van de coronaperiode (zie afbeelding 3 voor de beschikbare percentages).

 

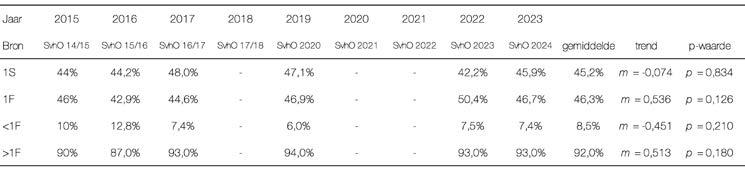
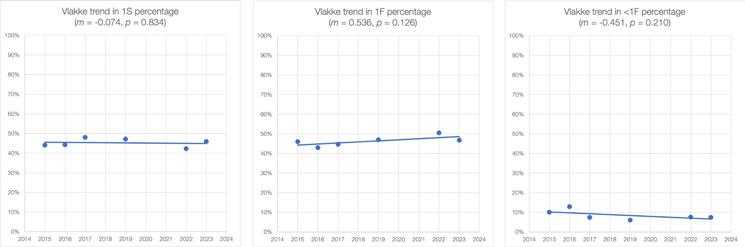
Ondanks deze beperkingen laten de beschikbare cijfers zien dat er geen duidelijke structurele verbetering of verslechtering is. De resultaten tonen lichte schommelingen, soms een kleine stijging, soms een daling, maar deze variaties zijn niet significant (zie tabel in afbeelding 3 voor de hoge p-waardes). Hierdoor kan voor de periode 2015-2023 het beste gesproken worden van een vlakke trend, waarbij geen aantoonbare vooruitgang of achteruitgang in de reken-wiskundeprestaties van groep 8-leerlingen wordt vastgesteld (afbeelding 4).

 

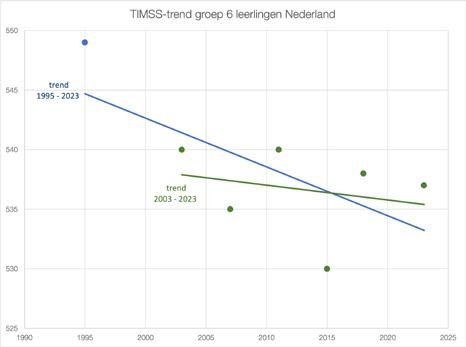
Stagnerende trend bij groep 6 (TIMSS) en laag niveau bij groep 8 (PEIL)

Naast de vlakke trend in eind/doorstroomtoetsen toont het internationale TIMSS-onderzoek een afvlakkende trend, waar deze eerst dalend was. Dit onderzoek meet de rekenvaardigheden van 10-jarige leerlingen in groep 6. Sinds 2003 zijn de TIMSS-scores stabiel gebleven rond 530-540 punten (Von Davier et al., 2024). Wanneer we echter terugkijken naar 1995, zien we dat de score destijds 549 punten was, een niveau dat Nederlandse leerlingen nooit meer hebben gehaald (Meelissen et al., 2020). De daling vond plaats tussen 1995 en 2003, waarna de prestaties stabiliseerden op een lager niveau. De trendlijn voor 2003-2023 daalt licht, maar wordt geleidelijk stabieler; de trend vlakt af (afbeelding 5).

 

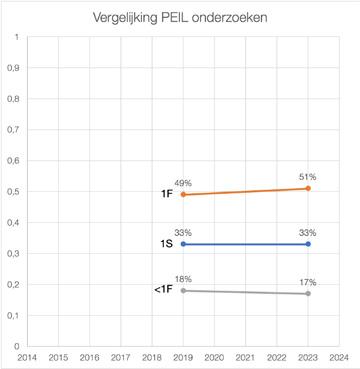
Het PEIL-onderzoek van de Inspectie van het Onderwijs, dat de rekenprestaties van groep 8 leerlingen monitort, laten met de resultaten van 2019 en 2023 een gelijk beeld zien: in beide jaren behaalde 33% van de leerlingen het 1S-niveau (Inspectie van het Onderwijs, 2021; 2024a). Het percentage leerlingen dat onder het 1F-niveau presteert, is nauwelijks veranderd (18% in 2019, 17% in 2023). Deze PEIL-onderzoeken worden afgenomen met low-stakes toetsen (‘toetsen zonder grote gevolgen’), via steekproeven onder een beperkt aantal scholen, waarvan de resultaten geen directe impact hebben op individuele leerlingen of scholen. Low-stakes toetsen kunnen de inzet van leerlingen beïnvloeden en maken de vergelijking met high-stakes toetsen lastig, omdat die vaak hogere scores opleveren, zoals bij de doorstroomtoets (Onderwijsraad, 2022). Hoewel er slechts twee metingen zijn en er dus niet van een trend gesproken kan worden, wijzen de resultaten op een stagnatie van te lage rekenvaardigheden op de basisschool, volgens deze twee PEIL-onderzoeken (afbeelding 6).

 

Stagnerende trend bij basisscholen

 

Trend bij scholen

Een trendanalyse op basis van alle Nederlandse groep 8 leerlingen of analyses uit (inter)nationale onderzoeken bieden een breed perspectief, maar zeggen weinig over en voor scholen. Voor scholen is het daarom effectiever om zich te richten op de meetbare referentieniveaus, waarbij de eigen schoolprestaties op de referentieniveaus een belangrijk houvast vormen voor de verbetering van het reken-wiskundeonderwijs, zoals ook beoogd werd door de Onderwijsraad. Voor dit artikel is in beeld gebracht hoeveel scholen het rekendoel behalen (>65% van de leerlingen beheersen 1S). Voor de laatste vier schooljaren is dat gedaan op basis van DUO onderwijsdata (afbeelding 7).

 

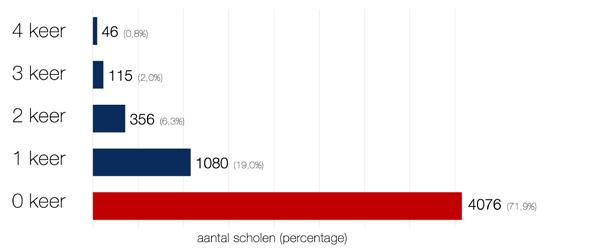
De analyse van het aantal scholen dat het 1S-rekendoel behaalt, laat zien dat structurele verbetering (nog) grotendeels uitblijft. De stagnatie is vooral zichtbaar bij 71,9% van de basisscholen die in vier jaar tijd geen enkel jaar het 1S rekendoel behaalde. Bovendien blijkt dat de scholen die het doel wél halen, dit vaak eenmalig doen. Hierbij gaat het om 19% van de scholen die een opwaartse lijn niet lijken voort te zetten. Slechts 9% van de scholen slaagt er meer dan één schooljaar in om de 1S-norm te halen, 6,3% haalt het tweemaal, 2% haalt het driemaal, en een fractie (0,8%) haalt het vier jaar op rij.

In vier jaar tijd lijkt er geen substantiële vooruitgang te zijn geboekt. Dit suggereert dat huidige inspanningen nog slechts beperkt effect sorteren en dat voor een grote groep scholen de uitdagingen onverminderd groot blijft. Dit duidt mogelijk op een fundamenteel probleem: incidentele succesvolle schooljaren lijken (nog) niet te leiden tot bestendiging van verbeteringen. Dit terwijl de ambitie van het ministerie van OCW om het 1S-doel te behalen wordt verhoogd, en de onderwijsinspectie strikter gaat onderzoeken of scholen de referentieniveaus behalen.

Dit roept de vraag op of scholen over voldoende kennis en middelen beschikken om het reken-wiskundeonderwijs duurzaam te verbeteren. Waarom leidt een succesvol schooljaar niet tot structureel betere reken-wiskundeprestaties over meerdere jaren? Mogelijk ligt het probleem in de inrichting en borging van het onderwijs, waardoor structurele verbeteringen uitblijven. Daarnaast rijst de vraag of de ambities van de referentieniveaus binnen de huidige onderwijspraktijk daadwerkelijk haalbaar zijn.

Zoals eerder aangegeven is het percentage leerlingen dat 1S moet behalen niet te hoog gekozen, maar weerspiegelt dat het doorstroompercentage. Een andere oorzaak zou dan kunnen zijn dat het reken-wiskundecurriculum te hoog gegrepen is. Dit zou pleiten voor een inhoudelijke versobering, maar dat zou betekenen dat het voortgezet onderwijs meer moet overnemen. Dat is onwenselijk, omdat leerlingen daar met complexere vakinhouden te maken krijgen. Het streven moet immers zijn om de lat hoog te leggen en daarom is het noodzakelijk om te investeren in beter reken-wiskundeonderwijs. In de aanbevelingen wordt onderbouwd dat het behalen van het 1S-niveau haalbaar is, mits de noodzakelijke randvoorwaarden worden gewaarborgd. Het identificeren en waarborgen van deze randvoorwaarden vereist nader onderzoek.

 

Aanbevelingen en conclusie

Om structurele vooruitgang in het reken-wiskundeonderwijs te realiseren, is een aanpak nodig die rekening houdt met zowel succesvolle factoren als de belemmeringen die scholen ervaren. De vier kernpunten uit het advies van de Onderwijsraad (Onderwijsraad, 1999b) kunnen daarbij leidend zijn en worden daarom hieronder als aanbevelingen beschreven.

 

Duidelijkheid voor scholen: focus op referentieniveaus

Een van de grootste uitdagingen voor scholen lijkt het gebrek aan een stabiele en effectieve aanpak binnen het reken-wiskundeonderwijs te zijn. Het huidige reken-wiskunde onderwijs lijkt onvoldoende aan te sluiten bij de specifieke behoeften van scholen die structureel onder de 1S-norm presteren.

Naast onderzoek naar wat werkt en niet werkt in het reken-wiskundeonderwijs (zie bijvoorbeeld: Hickendorff et al., 2019) kan nader onderzoek naar het gebruik van de referentieniveaus binnen scholen ook inzicht geven: in hoeverre vertalen scholen de referentieniveaus naar een heldere en consistente didactische aanpak voor rekenen-wiskunde? Hoe kunnen scholen beter ondersteund worden om hun aanpak en onderwijspraktijken op elkaar af te stemmen? Inzicht in de factoren die bijdragen aan stabiel goede resultaten van goed presterende scholen en hoe zij hun succesvolle aanpak hebben ontwikkeld en behouden, kan waardevolle inzichten opleveren. Wat doen deze scholen anders, en hoe kunnen andere scholen hiervan leren? Dit sluit aan bij bestaande bevindingen dat een deel van de basisscholen erin slaagt om structureel meer dan 65% van hun leerlingen op 1S-niveau te krijgen, terwijl andere scholen al jarenlang worstelen met lage resultaten. Casestudies naar deze goed presterende scholen kunnen inzicht bieden in cruciale succesfactoren, zoals de mate van instructie, de rol van automatiseren, de inzet van formatieve evaluatie, de rol van de schoolleider, en de rol van de rekencoördinator in het bewaken en bevorderen van onderwijsresultaten. Daarnaast kan onderzoek naar de mate waarin pabo-curricula en bijscholingsprogramma’s bijdragen aan een gedeeld en onderbouwd didactisch model binnen scholen inzicht geven. Als scholen fundamenteel verschillende rekenaanpakken hanteren zonder wetenschappelijke onderbouwing en/of zonder relatie met de referentieniveaus, ontstaat mogelijk een gefragmenteerde, niet onderbouwde praktijk die duurzame verbetering belemmert.

 

Gelijke kansen: waarborgen van rekenvaardigheid voor alle leerlingen

Gelijke kansen betekent dat alle leerlingen de benodigde basiskennis en -vaardigheden in rekenen-wiskunde eigenmaken. De huidige trends in schoolresultaten tonen echter aan dat een substantieel deel van de scholen er niet in slaagt om een deel van hun leerlingen op het benodigde 1S-niveau te krijgen. Hier rijst de vraag of er structurele factoren zijn die deze kloof veroorzaken, en hoe deze kunnen worden aangepakt. Zo kunnen het lerarentekort maar ook de impact van achtergrondfactoren zoals sociaaleconomische status en schoolweging op rekenresultaten inzicht geven. Waar sommige scholen met een hoge schoolweging erin slagen om toch bovengemiddelde resultaten te behalen, blijven andere ver achter. Maar zo zijn er ook scholen met een zeer lage schoolweging die er niet in slagen om de rekendoelen te realiseren. Inzicht in omvang, effect, en onderzoek naar deze verschillen kan helpen om te begrijpen welke interventies effectief zijn in het ondersteunen van kwetsbare leerlingen op verschillende typen scholen. Hierbij kan ook aandacht zijn voor de belemmeringen die scholen ervaren bij het doorvoeren van verbeteringen.

 

Transparantie: schooltrends en structurele verbeteringen

Transparantie in onderwijsresultaten is essentieel om inzicht te krijgen in de daadwerkelijke impact van de investeringen die gedaan zijn vanuit het masterplan basisvaardigheden. Een belangrijk aandachtspunt voor scholen zou dan moeten zijn hoe de rekenprestaties zich op langere termijn ontwikkelen, en welke trends zichtbaar zijn bij basisscholen. Hoewel sommige scholen incidentele verbeteringen laten zien, lijkt er op nationaal niveau nog geen structurele stijging te zijn die wijst op een brede vooruitgang van de schoolprestaties. Trendanalyse voor alle scholen kan waardevol inzicht bieden op schoolniveau. Hier is nader onderzoek naar de rekentrends van basisscholen van belang. Door systematisch schoolprestaties over meerdere jaren te analyseren, kan inzichtelijk worden gemaakt of er daadwerkelijk sprake is van een trendbreuk richting betere schoolresultaten. Daarbij kan in beeld gebracht worden welke scholen een negatieve, vlakke of positieve rekentrend hebben en welke verschillende factoren daar een rol bij spelen. Ook is het hierbij van belang om te onderzoeken welke belemmeringen scholen ervaren bij het verbeteren van hun reken-wiskundeonderwijs. Zijn dit factoren zoals onvoldoende vakinhoudelijke kennis bij leraren, lerarentekort, schoolweging of spelen andere factoren een grotere rol, zoals een te grote nadruk op het volgen van methodes? Door deze belemmeringen systematisch in kaart te brengen, kan gerichter ondersteuning geboden worden aan scholen die dit het meest nodig hebben.

 

Gerichte ondersteuning: wat scholen nodig hebben

Ten slotte is het cruciaal dat scholen die structureel onder de 1S-norm presteren, de juiste ondersteuning krijgen om verbeteringen door te voeren. De analyse van schoolresultaten laat zien dat een brede, consistente verbetering van het reken-wiskundeonderwijs tot op heden uitblijft. Dit roept de vraag op welke vormen van ondersteuning daadwerkelijk leiden tot duurzame verbetering. Een van de vragen hierbij is: welke ondersteuningsstrategieën werken voor scholen die jarenlang onder de norm presteren? Met welke interventies is een trendbreuk te realiseren van een negatieve of te lage vlakke schooltrend? Is bijvoorbeeld meer effect te behalen met intensieve schoolbegeleiding, of is een verandering in didactische aanpak werkzaam? Wat is de impact van meer vakinhoudelijke professionalisering van leraren op schoolniveau? Hier zou onderzoek naar verschillende professionaliseringstrajecten waardevolle inzichten kunnen opleveren.

 

Conclusie

De ontwikkeling van de kerndoelen laat een vicieuze cirkel zien van abstractie en concretisering, waarbij de belangrijkste tekortkoming het ontbreken van meetbare doelen is. Juist de meetbare doelen, in de vorm van referentieniveaus, bieden essentiële houvast voor scholen. De vier kernpunten uit het advies van de Onderwijsraad blijven onverminderd relevant voor de toekomst van beter functionerend reken-wiskundeonderwijs. Duidelijkheid met referentieniveaus kan scholen ondersteunen om hun onderwijs effectiever vorm te geven, terwijl gelijke kansen gewaarborgd kunnen worden door vroegtijdige en gerichte ondersteuning als reken-wiskunderesultaten achterblijven. Transparantie in schooltrends is nodig om de voortgang op schoolniveau te monitoren. En gerichte ondersteuning moet aansluiten bij de daadwerkelijke behoeften van scholen. Vervolgonderzoek is nodig om inzicht te krijgen in succesvolle schoolstrategieën, de impact van didactische keuzes en de structurele belemmeringen die verbeteringen in de weg staan. Alleen door deze factoren systematisch te onderzoeken en beleidsmatig op te pakken, kan de ambitie om de schoolprestaties op het gebied van rekenen-wiskunde structureel te verbeteren gerealiseerd worden. Zoals de Onderwijsraad ook in 2006 concludeerde: het streven moet zijn om de lat hoog te leggen, en niveaubewaking is daarbij een noodzakelijke voorwaarde (Onderwijsraad, 2006; Ledoux et al., 2009).