Leerresultaten einde basisonderwijs voor rekenen-wiskunde

In deze bijdrage volgt een nadere beschouwing van leerresultaten waarbij in de eerste plaats gekeken wordt naar enkele grote internationale vergelijkende onderzoeken waar Nederland al jaren aan meedoet: TIMSS en PISA. Daaruit blijkt dat deze resultaten over het geheel genomen stabiel hoog zijn en dat ons land al jaren een plaats in de subtop van internationale ranglijsten inneemt. Verder richten we de blik op de in Nederland regelmatig uitgevoerde peilingsonderzoeken waaruit eveneens blijkt dat van achteruitgang geen sprake is; in tegendeel, in de periode 2011-2023 zijn de resultaten licht gestegen. Daarnaast staan we stil bij oorzaken en gevolgen van de genoemde negatieve berichtgeving, waarbij onder meer vastgesteld wordt dat er de afgelopen jaren een soort ‘molensteeneffect’ van deze berichtgeving lijkt te zijn uitgegaan dat mogelijk tot een zekere ontmoediging en frustratie bij onderwijsgevenden en andere betrokkenen heeft geleid.

In het laatste deel van deze bijdrage richten we de blik op de toekomst. Zoals door veel auteurs wordt gemeld, behoeft het Referentiekader Doorlopende Leerlijnen en de daarin verwerkte vaardigheidsniveaus 1F en 1S anno 2025 een actualisering. Niet alleen lijkt het aan te bevelen de structuur van het kader in sommige opzichten te heroverwegen, ook sommige leerinhouden en -doelen behoeven aanpassing. Daarnaast is er een belangrijke evaluatieve kwestie: in hoeverre heeft het Referentiekader in de afgelopen jaren daadwerkelijk bijgedragen aan een soepele overgang van basis- naar voortgezet onderwijs, en dus aan het beoogde slechten van ‘drempels’ tussen deze onderwijsvormen? De voorgenomen actualisering, die momenteel door SLO wordt voorbereid, zal uiteindelijk moeten leiden tot herijking van de vaardigheidsniveaus 1F en 1S. In samenhang daarmee dienen bijpassende ‘ambities 2.0’ geformuleerd te worden die het genoemde molensteeneffect kunnen opheffen en die daarmee tot de nodige opluchting bij onderwijsgevenden kunnen leiden.

 

Inleiding: hardnekkige berichtenstroom

Veel betrokkenen zal het niet zijn ontgaan: er doet zich in de media een hardnekkige berichtenstroom voor dat er in het reken-wiskundeonderwijs in Nederland sprake is van een gestage achteruitgang in de leerresultaten einde basisonderwijs. Soms wordt dit bijna terloops gemeld (‘Rekenvaardigheden dalen snel op internationale ranglijsten’) in een artikel dat in essentie over een veel algemener onderwijsthema handelt[1] (afbeelding 1), en soms wordt het als een centraal thema in een actualiteitenrubriek opgevoerd (‘Het gaat niet goed met het rekenonderwijs’) zonder een spoor van onderbouwing of nuancering (Tegenlicht; afl. 1, september 2024)[2].  Onlangs verscheen in dit tijdschrift nog weer een artikel met (onder meer) een pleidooi voor ‘meetbare doelen voor rekenen-wiskunde’ waarin gesteld wordt dat ‘het behalen van de referentieniveaus voor veel leerlingen en scholen een uitdaging blijft’ en dat ‘structurele en doelgerichte verbetering van het reken-wiskundeonderwijs noodzakelijk is’ (Langerak, 2025)[3].

 

Een mogelijk gevolg van deze berichtenstroom is dat leraren basisonderwijs zich in toenemende mate onzeker over hun reken-wiskundeonderwijs gaan voelen. Ondanks een doorgaans ruime mate van vakbekwaamheid, gebaseerd op doordacht gebruik van de reken-wiskundemethode, ampele praktijkervaring en adequate interne begeleiding binnen de school[4], beginnen sommige leraren zich mogelijk af te vragen: doe ik het wel goed? Is mijn instructie wel toereikend? Zijn er andere onderwijsaanpakken die tot betere resultaten leiden?

In een vorige bijdrage in dit tijdschrift werd al betoogd dat het met die vermeende achteruitgang over het geheel genomen erg meevalt. Een analyse van de door de Inspectie gerapporteerde leerresultaten einde basisonderwijs laat zien dat er de afgelopen vijftien jaar in feite sprake is geweest van een bescheiden vóóruitgang van de resultaten (Buijs, 2024). Het percentage leerlingen dat referentieniveau 1F haalt, is in die tijd gestegen van ongeveer 85% naar 92%, terwijl het percentage leerlingen dat 1S haalt, van iets meer dan 40% naar 46% is gegaan (Ibid., p.47). In de jaarlijkse Inspectierapportages evenwel heeft steevast de nadruk gelegen op het feit dat die resultaten voor wat betreft het percentage leerlingen dat niveau 1S haalt, bij lange na niet beantwoorden aan de door de commissie Meijerink in 2008 geformuleerde ambitie van ongeveer 65% (Expertgroep doorlopende leerlijnen, 2008). Alleen in het onlangs gepubliceerde rapport ‘Staat van het Onderwijs 2025’ is de toonzetting enigszins aangepast en wordt gemeld dat de resultaten bij de in het schooljaar 2023-24 afgenomen Doorstroomtoets ongeveer gelijk zijn gebleven in vergelijking met voorgaande jaren (Inspectie van het Onderwijs, 2025a). Daarbij dient wel opgemerkt te worden dat die Doorstroomtoets vier maanden eerder in het schooljaar is afgenomen dan de in de voorafgaande jaren afgenomen Eindtoets, hetgeen impliceert dat de resultaten, indien geëxtrapoleerd naar een vergelijkbare afnameperiode, in feite hoogstwaarschijnlijk licht vooruit zijn gegaan[5].

Zoals in voornoemde bijdrage werd betoogd, berustte de ambitie van 65% op een waarschijnlijk onjuiste aanname dat dit percentage bij verschijning van het Doorlopende Leerlijnen-rapport in 2008 op ongeveer 50% lag, terwijl het werkelijke percentage iets meer dan 40% was. Evenzo is er sprake geweest van een waarschijnlijk onjuiste aanname dat het percentage op niveau 1F functionerende leerlingen in 2008 rond de 75% lag, terwijl dit in werkelijkheid op ongeveer 85% lag. Men kan uiteraard van mening verschillen over de vraag of een dergelijke bescheiden vooruitgang bevredigend is. Wat betreft de stijging van het percentage leerlingen dat niveau 1F haalt, behoeft daar weinig twijfel over te zijn – het lijkt aannemelijk dat Nederland in dat opzicht tot de wereldtop behoort. Meer discussie is er mogelijk over de vraag in hoeverre een verdere stijging van het percentage leerlingen dat niveau 1S haalt, gewenst is. Maar dat er wel degelijk sprake is geweest van een duidelijke stijging, staat buiten kijf.

Nu zou het nog kunnen dat deze stijging misschien voor einde basisonderwijs geldt, maar dat zich in de voorafgaande leerjaren of in de loop van het vervolgonderwijs wel degelijk ernstige schommelingen of zelfs een teruggang in de leerresultaten voordoet. Daarom nemen we in het eerste deel van dit artikel nog enkele andere informatiebronnen onder de loep. Dit betreft in de eerste plaats het grote internationale vergelijkende onderzoek TIMSS. Dit levert met name voor wat betreft de leerresultaten in groep 6 waardevolle aanvullende informatie op over het prestatieniveau van Nederlandse leerlingen ten opzichte van leerlingen in veel andere landen. Verder is er in de loop der jaren in Nederland een belangrijke serie zogeheten peilingsonderzoeken gehouden naar (onder meer) aspecten van het prestatieniveau, aanpakgedrag en de attitude van leerlingen. We staan stil bij de meest recente publicaties op dit terrein van december 2024 en april 2025 om na te gaan in hoeverre daarin dalingen worden gesignaleerd. Hoewel enigszins buiten het bestek van dit artikel, nemen we ook nog de leerresultaten voor wiskunde in klas 2 van het vervolgonderwijs onder de loep, zoals die naar voren komen in het eveneens internationale vergelijkende PISA-onderzoek.

In het laatste deel van dit artikel komen we eerst terug op de hierboven genoemde waarschijnlijk onjuiste inschatting van de percentages leerlingen in 2008 door de commissie Meijerink om na te  gaan waar deze onjuistheden mogelijk vandaan komen. We staan stil bij potentiële oorzaken en bij het ‘molensteeneffect’ dat hiervan de afgelopen jaren is uitgegaan. In het verlengde daarvan bespreken we in meer algemene zin de wenselijkheid cq. noodzaak om bepaalde aspecten van het Referentiekader Doorlopende leerlijnen dat als uitgangspunt voor de niveaus 1F en 1S fungeert, nog eens goed tegen het licht te houden en tot een zekere mate van actualisering van dit inmiddels ruim 17 jaar oude kader te komen, inclusief realistische en toekomstgerichte ‘ambities 2.0’. Daarmee zou tevens het genoemde molensteeneffect geleidelijk aan teniet gedaan kunnen worden.

 

TIMSS-resultaten 2023

In juni 2023 is de meest recente versie van de internationale TIMSS-toets in groep 6 in Nederland afgenomen[6]. Er deden voor rekenen-wiskunde in totaal 3555 leerlingen mee, verdeeld over 123 scholen (Von Davier et al., 2024; appendices B3 en B4). Aan alle voorgaande edities van het onderzoek deed Nederland ook met een representatieve steekproef mee, met uitzondering van 1999. Wel was het nu de tweede keer dat de toets geheel digitaal werd afgenomen, maar afgaande op de informatie van de Nederlandse onderzoekers die het onderzoek in ons land uitvoeren, is dat waarschijnlijk niet significant van invloed op de leerresultaten (Meelissen et al., 2020; Meelissen et al., 2024a). In afbeelding 2 is een overzicht te zien van de leerresultaten in Nederland door de jaren heen (Von Davier et al., 2024; Grade 4: Trends in Mathematics achievement). Duidelijk is te zien dat de resultaten voor ons land met uitzondering van het eerste afnamejaar 1995 in globale zin stabiel op hetzelfde niveau liggen, met in 2023 een score van 537 op een schaal die loopt van 400 tot 620.

 

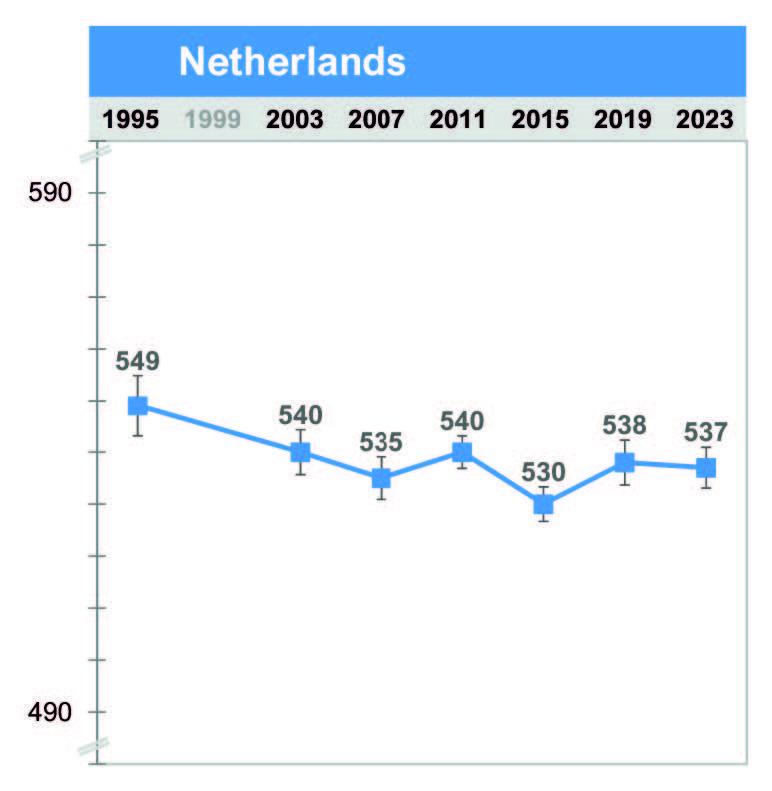
Kijken we naar het landenklassement (afbeelding 3; het totaal aantal deelnemende landen bedroeg 59), dan zit Nederland stabiel in wat de subtop van de mondiale ranglijst genoemd kan worden in een groepje landen zoals Roemenië, Letland, Noorwegen en Tsjechië.

 

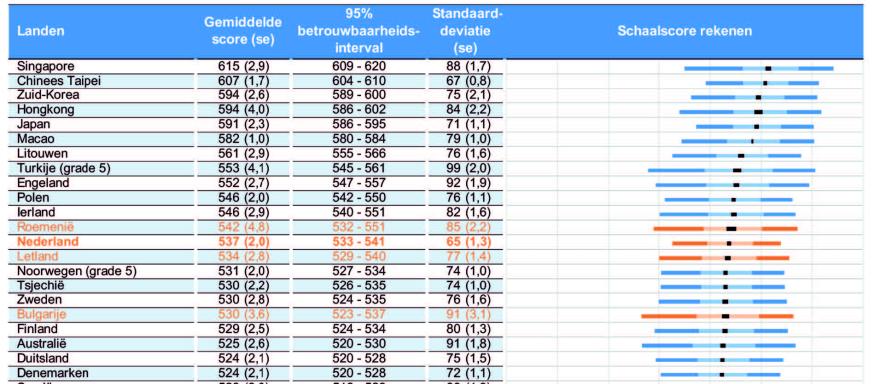
Opvallend is dat Nederland op de hele ranglijst een van de kleinste standaarddeviaties heeft, hetgeen erop wijst dat de verschillen tussen de zwakst en best presterende leerlingen in ons land relatief klein zijn. In vergelijking met voorgaande TIMSS-onderzoeken is de Nederlandse positie op deze ranglijst overigens nauwelijks veranderd – in 2019 bijvoorbeeld stond ons land met een score van 538 op de 14^e plaats, één plaats lager dan in 2023.

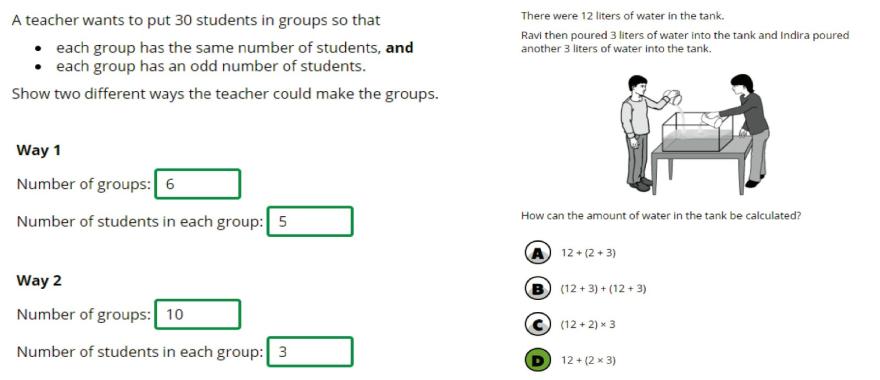
Verder dient nog opgemerkt te worden dat er discrepanties zijn tussen het binnen TIMSS aangehouden curriculum dat de basis vormt voor het ontwikkelen van de toets, en het in Nederland vigerende curriculum. Uit de door TIMSS uitgevoerde Test-Curriculum Matching Analysis (Von Davier et al., 2024; Appendix C, Exhibit C.2) blijkt dat de score voor Nederland 6 punten hoger uitgevallen zou zijn (543 in plaats van 537) als alleen de toetsopgaven waren meegerekend die corresponderen met het Nederlandse curriculum. Dit in tegenstelling tot bijvoorbeeld de Angelsaksische landen waarvoor geldt dat het TIMSS-curriculum vrijwel naadloos aansluit bij het nationale curriculum in die landen. In de analyse van Meelissen et al. van de TIMSS-resultaten van 2019 werd hier ook al een opmerking over gemaakt: ongeveer 73% van de TIMSS-toetsopgaven bleken in dat jaar aan te sluiten bij het Nederlandse curriculum (Meelissen et al., 2020, p.121). Bij de TIMSS-toets in 2023 lag dit percentage iets hoger, namelijk op 80% (Meelissen et al., 2024a, p.49). Dit betekent dat de Nederlandse leerlingen bij het maken van de toets in beide afnamejaren regelmatig tegen een type opgaven aanliepen dat in de rekenlessen niet was behandeld. Zie de twee voorbeelden[7] in afbeelding 4, afkomstig uit Mullis et al., 2020.

 

Al met al kan, afgaande op de TIMSS-resultaten van de afgelopen jaren, geconcludeerd worden dat Nederlandse leerlingen ook op het niveau van groep 6 goed presteren en dat zeker niet gesproken kan worden van een gestage daling van leerresultaten. De constatering van het in paragraaf 1 genoemde artikel over ‘snelle daling rekenvaardigheden op internationale ranglijsten’ lijkt dan ook grotendeels of geheel uit de lucht gegrepen.

 

Resultaten Peilingsonderzoek 2023 en in voorgaande leerjaren

Eens in de zoveel jaar wordt er in Nederland voor rekenen-wiskunde een zogeheten peilingsonderzoek uitgevoerd. Daarin worden niet alleen de leerresultaten op het niveau van einde basisonderwijs onderzocht, maar ook belangrijke andere onderwijsaspecten zoals aanpakgedrag van leerlingen, mate van plezier in rekenen, verschillen tussen jongens en meisjes en domeinspecifieke resultaten[8]. De meest recente peiling, afgenomen in 2023, is uitgevoerd onder 3382 leerlingen op 106 scholen met regulier basisonderwijs (Inspectie van het Onderwijs, 2024a; Meelissen et al., 2024b). Het onderzoek wijst in de eerste plaats uit dat de rekenvaardigheid van de leerlingen in groep 8 in vergelijking met 2019 (het vorige peilingjaar) ongeveer gelijk is gebleven (Inspectie van het Onderwijs, 2024a, p.108; Punter, 2025). Dit ondanks de tussenliggende periode van de pandemie die ervoor gezorgd heeft dat nogal wat scholen met name in het schooljaar 2021-22 een deel van de tijd zelfs helemaal dicht is geweest (Inspectie van het Onderwijs, 2024a, p.125), waarbij slechts een zekere mate van ‘onderwijs op afstand’ werd gegeven. Blijkbaar is een eventuele leerachterstand als gevolg van dat beperkte onderwijsaanbod in het daarop volgende schooljaar 2022-23 alweer grotendeels weggewerkt. Gecombineerd met het feit dat de leerresultaten in de voorafgaande periode 2011-2019 licht waren gestegen (Inspectie van het Onderwijs, 2021, p.113), betekent dit dat er over de hele periode 2011-2023 sprake is geweest van een lichte stijging in de resultaten, en dus zeker niet van een daling.  

Verder zijn blijkens het peilingsonderzoek van 2023 de percentages leerlingen die voor wat betreft de referentieniveaus respectievelijk onder niveau 1F, op niveau 1F en op niveau 1S scoren, eveneens gelijk gebleven in vergelijking met 2019. Opmerkelijk is wel dat deze percentages nogal afwijken van de bij het onderzoek naar de resultaten van de eindtoets in 2023 gevonden percentages. Behaalde volgens dat laatste onderzoek ruim 92% van de leerlingen niveau 1F (Inspectie van het Onderwijs, 2024b, p.19), volgens het peilonderzoek zou dit maar 84% zijn. En bleek bij het onderzoek naar de eindtoetsresultaten dat ruim 45% van de leerlingen niveau 1S beheerste (Ibid., p.20), bij het peilingsonderzoek was dit maar 33%. Als verklaring voor deze discrepanties wijzen de onderzoekers op het feit dat het bij het peilingsonderzoek om een ‘low stake-toets’ gaat waarbij niets op het spel staat terwijl het bij de eindtoets om een ‘high stake-toets’ gaat waar juist veel op het spel staat (Inspectie van het Onderwijs, 2024a, p.109). Van de uitkomsten van deze laatste toets hangt immers de eigen onderwijstoekomst van de leerlingen voor een deel af. Bovendien wordt er door de scholen vaak maandenlang naar de eindtoets toegewerkt om de leerlingen tot een optimaal resultaat in staat te stellen. In het geval van het peilingsonderzoek daarentegen is de toetsafname weinig meer dan een soort tussendoortje voor de leerlingen. De verschillen tussen low stake- en high stake-toetsen worden door internationaal onderzoek bevestigd. Zo wijst Finn erop dat de motivatie van leerlingen bij low stake-toetsen vaak beduidend lager is dan bij high stake-toetsen (Finn, 2015). En Pools en Monseur (2021) laten zien dat leerlingen vooral in het laatste deel van een low stake-toets geneigd zijn om het bijltje er vrij snel bij neer te gooien. Het ligt dus voor de hand dat de uitkomsten van het peilingsonderzoek beduidend lagere beheersingspercentages voor de niveaus 1F en 1S laten zien. Dit wijst erop dat je de resultaten van het peilingsonderzoek wel kunt vergelijken met de resultaten van voorgaande peilingsonderzoeken, net zoals je de resultaten van eindtoetsonderzoeken uit verschillende jaren onderling kunt vergelijken, maar niet de resultaten uit het ene type onderzoek met die uit een ander type onderzoek. 

Het in 2025 uitgebrachte rapport Peil.taal en rekenen (Inspectie van het Onderwijs, 2025b) bevat geen resultaten van nieuw peilingsonderzoek zoals de  titel doet vermoeden, maar een overzicht van de resultaten en achtergronden bij de in 2024 voor het eerst uitgevoerde Doorstroomtoets. Ook in het tegelijkertijd uitgebrachte rapport Staat van het Onderwijs 2025 (Inspectie van het Onderwijs, 2025a) worden deze resultaten besproken. Zoals in de inleiding van het peil-rapport wordt gemeld, zijn de  gerapporteerde resultaten bij deze Doorstroomtoets niet goed vergelijkbaar met de resultaten op de in de voorafgaande jaren afgenomen Eindtoetsen. Dit is het gevolg van een andere normeringswijze én van het feit dat de Doorstroomtoets eerder in het leerjaar is afgenomen dan de Eindtoetsen. Dit scheelt feitelijk vier maanden onderwijstijd in groep 8 (afnameperiode eind januari/begin februari versus eind april/begin mei), hetgeen het vermoeden doet rijzen dat de resultaten op de Doorstroomtoets nog beduidend hoger hadden kunnen uitpakken als deze toets in een vergelijkbare afnameperiode was afgenomen en de leerlingen 4 maanden langer de tijd hadden gehad om zich de leerstof verder eigen te maken. (Zie ook de opmerkingen hierover in de Inleiding van dit artikel en in noot 5).

 

PISA-resultaten 2022

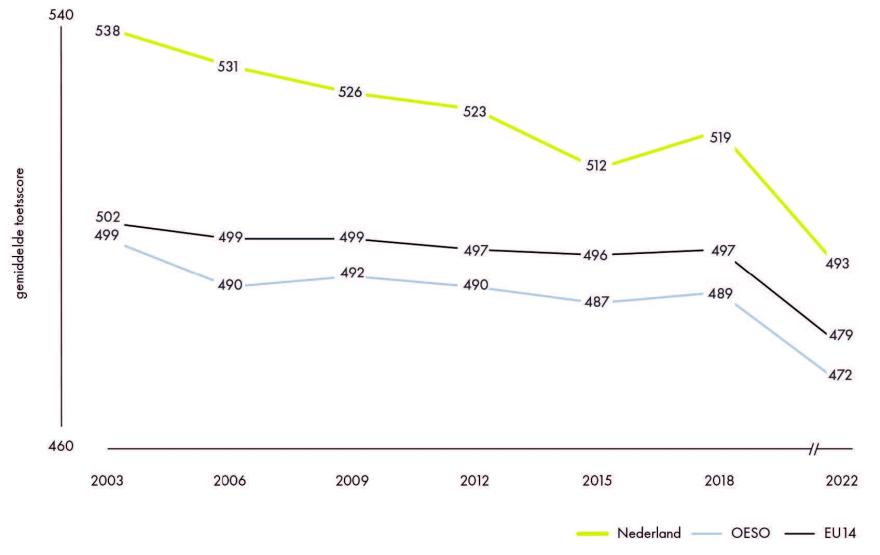
Kijken we vervolgens nog naar de leerresultaten van het PISA-onderzoek van 2022, dan kan ook daar vastgesteld worden dat Nederland qua prestatieniveau voor 15-jarige leerlingen in het voortgezet onderwijs (wiskunde[9]) eveneens in de subtop van de mondiale ranglijst zit (Meelissen et al., 2023). Zie afbeelding 5; het totale aantal deelnemende landen bedroeg 81.

 

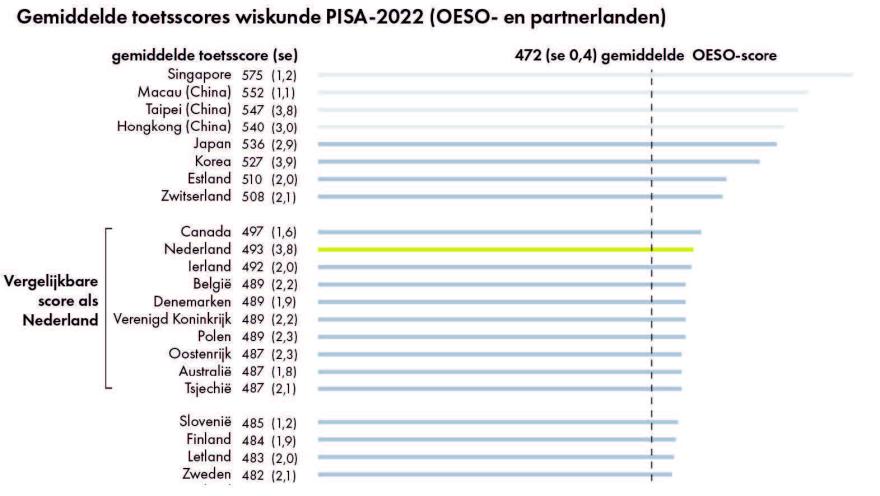
Hierbij moet worden opgemerkt dat zich in de Nederlandse PISA-leerresultaten door de jaren heen wel een zekere dalende tendens voordoet (let wel, de y-as is sterk ingekort: de daling is aanzienlijk kleiner dan de grafiek suggereert). Dit is met name het geval in de periode 2018-22 (afbeelding 6; Ibid., p.21). Gezien het feit dat deze dalende tendens zich op een vergelijkbare manier in veel van de aan het PISA-onderzoek deelnemende landen voordoet, lijkt echter aannemelijk dat deze tendens mede veroorzaakt is door de pandemie en de (vooral in het vervolgonderwijs) veelvuldig voorkomende schoolsluitingen in deze periode. In dezelfde periode deed zich in de leerresultaten einde basisonderwijs immers een vergelijkbare daling voor die in de jaren na de pandemie alweer weggewerkt is (Inspectie van het Onderwijs, 2024b, p.43; Inspectie van het Onderwijs 2025a, p.40).

 

Het ‘molensteeneffect’ van de ambities uit 2008; noodzaak tot actualisering van het Referentiekader

 

Wat er mogelijk is misgegaan bij het inschatten van de percentages in 2008; het molensteeneffect

In het specifiek aan rekenen-wiskunde gewijde rapport van de Commissie Meijerink (Expertgroep doorlopende leerlijnen, 2008) wordt duidelijk gemaakt dat veel in het werk gesteld is om op basis van de expertise van diverse betrokkenen en analyse van uiteenlopende bronnen, zoals relevante leerplandocumenten, lesmaterialen, resultaten van nationale peilingsonderzoeken en internationale vergelijkingsonderzoeken, tot een zorgvuldige afbakening van de beoogde referentieniveaus te komen en passende ambities voor verhoging van leerresultaten te formuleren.

Maar bij het vaststellen van die ambities lijkt het mis te zijn gaan. Immers, men heeft een inschatting gemaakt dat ten tijde van het onderzoek het percentage op niveau 1F presterende leerlingen (de ‘basiskwaliteit’ voor het funderend onderwijs) rond de 75 lag. Dat wil dus zeggen dat ongeveer 75% van de leerlingen de verzameling opgaven die als kenmerkend voor niveau 1F werden gekwalificeerd, goed maakte. Evenzo schatte men in dat het percentage op niveau 1S presterende leerlingen (de ‘streefkwaliteit’) rond de 50 lag. Ergo: dat ongeveer 50% van de leerlingen de verzameling opgaven die als kenmerkend voor niveau 1S werden gekwalificeerd, goed maakte. Terwijl het er, gelet op de bevindingen in de eindtoetsonderzoeken uit de daarop volgende jaren 2008-12 (zie bijvoorbeeld Inspectie van het Onderwijs, 2015; Hemker, 2015;  Inspectie van het Onderwijs, 2017; Buijs, 2024), alle schijn van heeft dat het eerstgenoemde percentage in werkelijkheid aanzienlijk hoger heeft gelegen (namelijk rond de 85%) en het tweede percentage beduidend lager (namelijk rond de 40%). Met als gevolg dat de ambitie met betrekking tot het percentage op niveau 1F presterende leerlingen feitelijk helemaal geen ambitie was, en dat de tweede ambitie nogal onrealistisch was en mede daardoor in de volgende decennia als een soort molensteen om de nek van het onderwijs heeft gehangen. Men zou in dat opzicht van een soort ‘molensteeneffect’ kunnen spreken: steeds weer werd in de Inspectierapportages de nadruk gelegd op het feit dat met name de voor niveau 1S uitgesproken ambitie nog verre van gerealiseerd was, en steeds weer werd deze constatering in de media vervolgens breed uitgemeten als een signaal dat het niet goed gaat met het reken-wiskundeonderwijs.

De vraag dient zich dan aan waar het bij het maken van de genoemde inschattingen en de daaruit voortvloeiende ambities mogelijk mis is gegaan. En, in samenhang daarmee: In hoeverre nog andere aspecten van het Referentiekader Doorlopende Leerlijnen, in aanmerking zouden kunnen komen om nog eens goed tegen het licht te houden teneinde tot een zekere mate van actualisering te komen. Dit zou ook met zich mee kunnen brengen dat het molensteeneffect dat deze inschattingen indirect teweeg gebracht hebben, geleidelijk aan teniet gedaan zou kunnen worden. 

In het rapport wordt over de werkwijze bij het maken van de inschattingen het volgende gemeld (p.24):

‘De beschrijvingen van de referentieniveaus zijn op inhoudelijke overwegingen geformuleerd en worden exemplarisch toegelicht met opgaven die goed gemaakt moeten worden. De meeste voorbeeldopgaven bij de twee referentieniveaus 1F en 1S zijn ontleend aan het meest recente PPON-onderzoek. Dat maakt het mogelijk om tegelijk de haalbaarheid van de voorbeeldopgaven te beoordelen en de ambitie tot niveauverhoging vast te leggen. De geselecteerde voorbeeldopgaven van het referentieniveau 1F worden op dit moment door 25% van de leerlingen niet goed gemaakt, zodat hier de ambitie is om zoveel mogelijk van die 25% naar het minimale basisniveau te krijgen. (…) De streefkwaliteit 1S is bedoeld voor leerlingen in groep 8 met rekenpotentie voor vmbo theoretisch en havo-vwo, terwijl de geselecteerde voorbeeldopgaven op dit moment door 50% van de leerlingen niet goed worden gemaakt. Omdat op dit moment een 65% van de leerlingenpopulatie doorstroomt naar vmbo-t of havo-vwo, is hier de ambitie om nog eens 15% van de leerlingenpopulatie op het niveau van het referentieniveau 1S te laten presteren.’

Verderop in het rapport (p. 31) wordt deze werkwijze als volgt toegelicht:

‘De PPON-opgaven zijn aan deskundigen voorgelegd die er een bepaalde standaard over een wenselijk niveau van beheersing aan hebben toegekend. Harskamp stelt in zijn rapport aan de Expertgroep: ‘Nadeel van deze manier van ontlokken van uitspraken bij deskundigen is dat men op deze manier een (inter)subjectief wenselijke situatie krijgt voorgeschoteld. De standaarden zijn niet expliciet gebaseerd op de vereiste entreeniveaus in het vervolgonderwijs en men mag daarom twijfelen aan de validiteit (voorspellende waarde) van de standaarden voor de schoolloopbaan’. Anderen (Van de Craats, 2007) wegen dat oordeel van de deskundigen wel zwaar mee in de beoordeling van de kwaliteit van de uitstroom van het basisonderwijs. Als werkgroep hebben we voor het domein rekenen & wiskunde zowel de empirische gegevens (wie kan deze opgave nu goed maken) als ons inhoudelijk oordeel en onze kennis van het basisonderwijs en het voortgezet onderwijs meegewogen in de uiteindelijke beschrijving van de beide eerste referentieniveaus 1F en 1S.’

Blijkbaar heeft men uit het PPON-onderzoek van 2004 dus twee selecties van voorbeeldopgaven genomen die als maatgevend voor de beoogde referentieniveaus 1F en 1S werden aangemerkt en die in dat PPON-onderzoek door resp. 75% van de leerlingen (opgaven niveau 1F) en 50% van de leerlingen (opgaven niveau 1S) goed gemaakt werden. Aan deze twee selecties heeft men andere typen opgaven toegevoegd die naar het oordeel van de commissieleden eveneens van grote waarde waren om als ijkpunt te hanteren voor verdere ‘kwaliteitsverbetering  van de uitstroom’ uit het basisonderwijs.

Bij deze werkwijze zijn duidelijk enkele kritische kanttekeningen te plaatsen. In de eerste plaats, de gegevens over de percentages leerlingen stamden uit 2004, dus er zat een gat van 4 jaar tussen het moment van het PPON-onderzoek en de publicatie van het rapport van de commissie Meijerink in 2008. Wat er in de tussenliggende jaren met het prestatieniveau is gebeurd, is onbekend en niet ‘meegenomen’ bij de inschatting van de beheersingspercentages.

In de tweede plaats was een deel van de opgaven die door de commissie als opgaven van 1S-niveau werden gekwalificeerd, niet afkomstig uit het PPON-onderzoek maar uit andere bronnen. De kwalificatie als 1S-opgaven werd dus deels toegekend op basis van intersubjectieve consensus door de commissieleden en geraadpleegde andere deskundigen, en niet op basis van het feit dat deze opgaven cruciaal zouden zijn voor een succesvolle overgang van basisonderwijs naar voortgezet onderwijs. Zoals ook door Harskamp werd geoordeeld, was het gevaar van subjectiviteit dus zeker niet denkbeeldig[10].

En in de derde plaats was de steekproef van de PPON-2004 (in totaal 3078 leerlingen) niet helemaal representatief voor de totale toenmalige leerlingenpopulatie van groep 8. Scholen met een populatie met een relatief hogere sociaal-economische achtergrond van de schoolbevolking waren enigszins oververtegenwoordigd, en scholen met een populatie met een relatief lagere sociaal-economische achtergrond van de schoolbevolking juist ondervertegenwoordigd (Janssen, Van Weerden & Scheltens, 2005, p.25-26). Met als mogelijk gevolg, dat het percentage op niveau 1S presterende leerlingen te hoog is ingeschat, terwijl het percentage op niveau 1F presterende leerlingen juist te laag is ingeschat. Dit zou dus goed kunnen verklaren waarom de ambitie voor verhoging van het percentage op 1S-niveau presterende leerlingen te hoog is geweest, terwijl de ambitie voor verhoging van het percentage 1F-leerlingen juist te laag is genomen.

Al met al lijkt het aannemelijk dat zich in de werkwijze van de commissie Meijerink op het punt van de inschatting van de beheersingspercentages van de niveaus 1F en 1S een zekere mate van onnauwkeurigheid heeft voorgedaan, waardoor deze inschattingen niet voldoende maatgevend zijn geweest voor de feitelijke toenmalige percentages leerlingen die deze niveaus in 2008 zouden beheersen.  Op zich doet dit natuurlijk niet veel af aan de betekenis van het referentiekader als een middel om tot een verhoging van het prestatieniveau in het reken-wiskundeonderwijs te komen[11]. Maar op één punt waren de gevolgen van deze onnauwkeurigheid wel ingrijpend: door de nadruk die in de loop der jaren door de Inspectie in de jaarlijkse Staat van het Onderwijs-rapportages telkens weer op het niet halen van de 1S-ambitie is gelegd (en de daaruit voortvloeiende berichtenhausse in de media), is deze ambitie steeds meer als een molensteen om de nek van het onderwijs gaan hangen. Met als bedenkelijke bijkomende schade dat nogal wat scholen en leraren mogelijk steeds meer zijn gaan twijfelen aan de kwaliteit van hun eigen onderwijs. Uiteraard kan dit nooit de bedoeling van het Referentiekader zijn geweest.

 

De noodzaak tot actualisering van het Referentiekader

Nu valt het ook in meer algemene zin natuurlijk te bezien in hoeverre het Referentiekader 17 jaar na dato toe is aan een zekere mate van actualisering en herijking. Zijn er bepaalde leerstofonderdelen waarvan de beheersing minder relevant is (geworden) voor een soepele overgang van basis- naar voortgezet onderwijs dan destijds werd aangenomen? Zijn er andere soorten leerstof of leerdoelen die anno 2025 in het kader opgenomen zouden moeten worden? Is de dubbele inkadering van de leerinhouden zoals die in het Referentiekader wordt gehanteerd (met voor elk domein een dubbele drieslag aan inhoudsaspecten en beheersingsdoelen; zie het voorbeeld in afbeelding 7) nog wel actueel? 

 

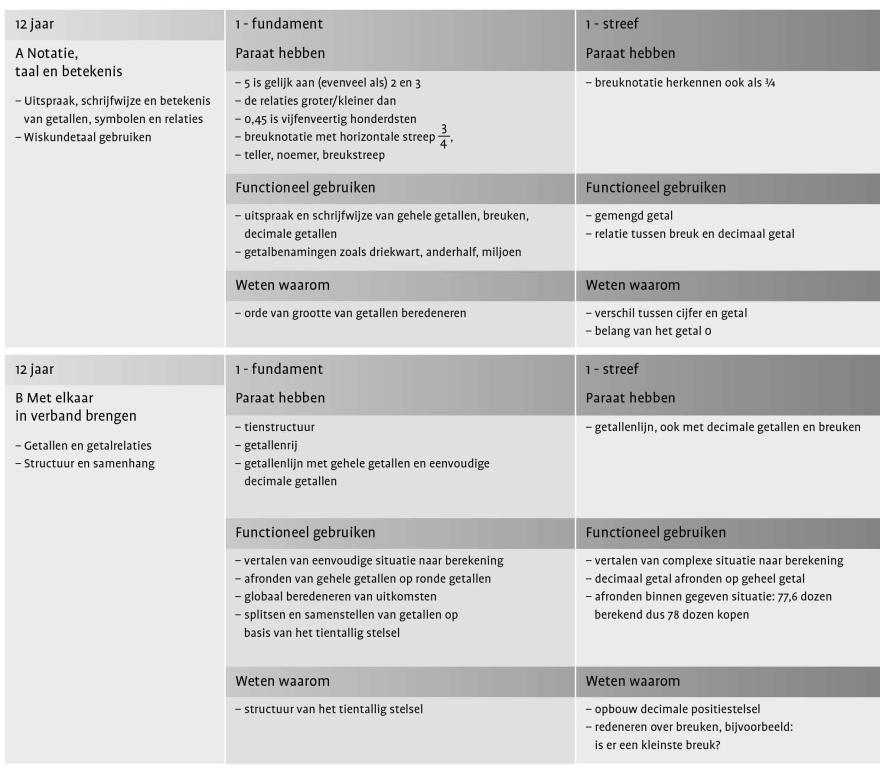
In de afgelopen jaren hebben diverse auteurs erop gewezen dat actualisering inderdaad wenselijk en nodig is. Zo laten Van den Broek et al. (2022) in hun ‘Analyse en evaluatie referentieniveaus Nederlandse taal en rekenen’ zien dat de hierboven genoemde dubbele inkadering op sommige punten verwarrend werkt. Als voorbeeld noemen zij het gebruik van de termen ‘Gebruiken’ en ‘Functioneel gebruiken’ (p.34). Ook signaleren zij dat de gehanteerde terminologie soms tekort schiet. Zo wordt de term ‘rekenen’, die door het hele kader heen frequent voorkomt, niet correct gebruikt omdat het Referentiekader ook niet-rekenkundige domeinen zoals Meten en meetkunde en Verbanden omvat (p.36). Tevens constateren zij dat er nogal wat ruimte voor interpretatieverschillen van de voorbeelden uit de concretiseringen is als deze als doel op zich in plaats van als voorbeeld worden geïnterpreteerd (p.38).

Verder wordt in diverse publicaties benadrukt dat de prestaties van Nederlandse leerlingen op het gebied van ‘wiskundig probleemoplossen’ duidelijk voor verbetering vatbaar zijn en dat daar in een volgende versie van het Referentiekader meer aandacht voor zou moeten zijn (Gravemeijer & Van Galen, 2020; Inspectie van het Onderwijs, 2024a en 2025a; Van Zanten, 2025). Hetzelfde geldt voor onderwerpen die in het Referentiekader geheel ontbreken zoals kritisch omgaan met grote hoeveelheden data en modelleren. Ook wijzen sommige auteurs erop dat de term ‘basisvaardigheden’ als gevolg van maatschappelijke en technologische ontwikkelingen een andere interpretatie behoeft en minder gefocust moet zijn op bijvoorbeeld beheersing van standaardprocedures met hele getallen en kommagetallen (Hoogland, 2024). In dat kader pleiten Gravemeijer en Van Galen (2024) ervoor om de nadruk in het onderwijs veel meer te leggen op wat zij noemen het ‘flexibel kunnen gebruiken van rekenoperaties in toepassingssituaties’ en veel minder op het inslijpen van standaardprocedures. Deze spelen immers, aldus deze auteurs, in de door hen  geanalyseerde toetsen uit het peilingsonderzoek maar ook in het vervolgonderwijs en in het leven van alledag nog maar een zeer beperkte rol.

Daarnaast is er een belangrijke evaluatieve kwestie. Een van de hoofddoelen van het Referentiekader is het bevorderen van een soepele overgang van de ene naar de andere onderwijsvorm, cq. het wegnemen van ‘drempels’. Zijn er aanwijzingen dat het kader in deze zin inderdaad een positief effect heeft (gehad)? En dat leerlingen die bijvoorbeeld in groep 8 op niveau 1S functioneren inderdaad een voorspoedige schoolloopbaan in het voortgezet onderwijs doormaken terwijl dit bij leerlingen die op een lager niveau functioneren maar toch naar vmbo-t of havo/vwo doorstromen, minder het geval is? Mochten zulke aanwijzingen niet te vinden zijn, dan zou nagegaan kunnen worden hoe een volgende versie van het Referentiekader, in combinatie met andere beleidsmaatregelen, op een meer effectieve wijze ingericht kan worden.  

Tenslotte is het natuurlijk aan te bevelen om een goede afstemming tussen de onlangs gepubliceerde nieuwe generatie concept-kerndoelen (SLO, 2024a) en een geactualiseerde versie van het Referentiekader tot stand te brengen. In deze concept-kerndoelen wordt bijvoorbeeld een geheel andere domeinindeling gepresenteerd (met een driedeling in ‘wiskundige concepten’, ‘wiskundige denk-werkwijzen’ en ‘wiskunde en de wereld’; afbeelding 8) dan de in het Referentiekader aangehouden vierdeling. Ook worden andere accenten gelegd, zoals dat er meer aandacht is voor samenhang, zowel binnen het gebied rekenen-wiskunde zelf als met andere leergebieden (Ibid., p.6-7). Daarnaast is er bij de doelbeschrijvingen ruime aandacht voor actuele onderwerpen zoals kritisch omgaan met grote hoeveelheden data, probleem oplossen en wiskundig modelleren[12] – zaken die in het Referentiekader zoals eerder opgemerkt vrijwel ontbreken. Het lijkt dan ook zeker geen overbodige luxe om beide publicaties grondig op elkaar af te stemmen.

 

Op weg naar realistische ambities 2.0

Gelukkig zijn de hierboven geschetste ontwikkelingen ook het ministerie van OCW niet ontgaan. Aan SLO is inmiddels een ‘werkopdracht actualisatie referentieniveaus taal en rekenen’ verstrekt waarbij een ‘impactanalyse van het huidige referentiekader in relatie tot de bijgestelde kerndoelen’ uitgevoerd dient te worden (SLO, 2024b). De resultaten van deze analyse dienen vervolgens gecombineerd te worden met inzichten uit de evaluatie van het Referentiekader uit 2022 (cq. de hierboven genoemde ‘Analyse en evaluatie referentieniveaus’ van Van den Broek et al., 2022) om tot adviezen te komen over mogelijke aanpassingen van het Referentiekader. Daarna zal een vervolgopdracht gegeven worden met richtlijnen voor deze aanpassingen.

Het zal duidelijk zijn dat een dergelijke actualisering ook consequenties heeft voor de beide vaardigheidsniveaus 1F en 1S – ook deze zullen op termijn herzien moeten worden, met als gevolg dat er tevens aangepaste, toekomstgerichte ambities 2.0 voor verhoging van het onderwijsniveau en leerresultaten geformuleerd dienen te worden. Gelet op eerdere discussies over deze problematiek zal dit nog wel de nodige voeten in de aarde hebben. Maar áls het dan uiteindelijk zo ver is, is de kans ook groot dat het hierboven aangeduide molensteeneffect waar het onderwijs geruime tijd last van heeft gehad, geleidelijk aan tot het verleden gaat behoren. Voor veel praktijkmensen, begeleiders en andere betrokkenen zou dit een niet geringe opluchting kunnen zijn.

 

 

[1] Zie het artikel ‘De kracht van kennis’ in het Alumnimagazine van Universiteit Utrecht waarin een pleidooi voor ‘betrokken en gepassioneerde docenten met gedegen vakkennis’ wordt gehouden (Schuring, 2024). 

[2] In deze aflevering van Tegenlicht meldt eerst een ambtenaar van OCW dat ‘het niet goed gaat met het rekenonderwijs’ en dat ‘er sprake is van dalende prestaties’. Naderhand komt een vertegenwoordiger van een particuliere bijlesschool (het ‘Nederlands Mathematisch Instituut’) aan het woord die een vorm van rekenonderwijs lijkt voor te staan waarin het kale rekenen centraal staat dat in Nederland in de jaren ’60 en ’70 van de vorige eeuw in zwang was.

[3] Ongelukkigerwijs wordt op geen enkele manier gespecificeerd wat met ‘meetbare doelen’ bedoeld wordt, of wat meetbare van onmeetbare doelen onderscheidt. Verder lijkt het pleidooi volledig voorbij te gaan aan het feit dat het Referentiekader Doorlopende leerlijnen inmiddels ruim 17 jaar oud is en duidelijk toe is aan actualisering zoals in de afgelopen jaren door diverse auteurs is benadrukt. Zie bijvoorbeeld Van den Broek et al., 2022, waarin verschillende verwarrende en gedateerde aspecten van het Referentiekader op een rij worden gezet. Zie ook paragraaf 5.2 van dit artikel.

[4] Blijkens het peilingsonderzoek 2022-23 heeft momenteel 84% van de basisscholen een rekencoördinator die onder meer taken heeft wat betreft het bijdragen aan nieuwe ontwikkelingen binnen het rekenonderwijs, regelmatige evaluatie van het gebruik en de opbrengsten van de rekenmethode, en het bijdragen aan de ontwikkeling van rijke leeromgevingen voor rekenen-wiskunde op school (Inspectie van het Onderwijs, 2024a, p.46-47).

[5] De Eindtoets werd de afgelopen jaren gewoonlijk in de periode eind april-begin mei afgenomen. De Doorstroomtoets daarentegen werd in het schooljaar 2023-24 afgenomen in de periode eind januari-begin februari, dus 4 maanden eerder. Dit betekent dat de leerlingen in dat schooljaar 4 maanden minder de tijd hebben gekregen (bijna 40% van de netto-onderwijstijd in dat jaar) om zich, ter voorbereiding op de toets, de leerstof eigen te maken. Het lijkt aannemelijk dat dit een negatief effect op de resultaten gehad moet hebben en dat deze resultaten, bijvoorbeeld voor wat betreft het percentage op niveau 1S functionerende leerlingen, zeker enkele procenten hoger uitgevallen zouden zijn indien de afnameperiode gelijk was gebleven aan die in voorgaande jaren. Met daarbij nog de kanttekening dat dit verschil van vier maanden in afnameperiode in het Staat van het Onderwijs 2025-rapport in het geheel niet wordt vermeld, maar alleen terloops in het tegelijkertijd verschenen rapport ‘Peil.Taal en rekenen. Einde basisonderwijs en speciaal (basis)onderwijs 2023-2024’ (zie Inspectie van het Onderwijs, 2025b, p.2).

[6] Behalve voor rekenen-wiskunde wordt er in groep 6 ook een toets voor natuurwetenschappen (‘science’) afgenomen. Verder wordt er in klas 2 van het voortgezet onderwijs voor wiskunde ook een toets afgenomen. We laten de resultaten daarvan hier buiten beschouwing.

[7] De antwoorden van deze opgaven, afkomstig uit Mullis et al., 2020, staan al in de opgaven aangegeven (groen).

[8] Het kan belangrijk zijn om juist deze domeinspecifieke trends boven tafel te krijgen omdat daarmee een veel genuanceerder beeld van de stand van zaken met betrekking tot mogelijke stijgingen en dalingen in het vaardigheidsniveau gecreëerd kan worden – trends die soms ‘verdoezeld’ worden als alleen op een meer globaal niveau naar leerresultaten wordt gekeken. Zie de interessante analyse van Van Weerden et al., 2016, naar aanleiding van 25 jaar PPON-onderzoek.

[9] Anders dan bij TIMSS ligt de nadruk qua leerstofinhoud bij PISA op wat genoemd wordt ‘wiskundige geletterdheid’ met veel aandacht voor het toepassen van reken/wiskundige vaardigheden en probleemoplossen. Zie pisa2022-maths.oecd.org.

[10] Zie voor een nadere analyse van deze kwestie zoals door Harskamp gemaakt, bijlage 1 bij het Doorlopende Leerlijnenrapport, p.98-101.

[11] Het moge overigens duidelijk zijn dat onderwijsbeleid waarin ambities met betrekking tot niveauverhoging van leerresultaten wordt geformuleerd, ten allen tijde gepaard dient te gaan met andere beleidsmaatregelen op het gebied van bijvoorbeeld nascholing, ontwikkeling en opleiding.

[12] Het belang van dergelijke ‘denk-werkwijzen’ wordt in het Toelichtingsdocument van de concept-kerndoelen nader toegelicht en onderbouwd vanuit een internationaal perspectief. Zie SLO (2024), Toelichtingsdocument p.24-25 en p.40-41.