Reken het rekenonderwijs niet af op percentages leerlingen die 1S behalen

Aanleiding voor een brede probleemanalyse

Over het rekenniveau van leerlingen aan het einde van het basisonderwijs bestaat al jaren veel discussie. De laatste tijd worden de opbrengsten van het reken-wiskundeonderwijs steeds vaker afgemeten aan de percentages leerlingen die streefniveau 1S behalen, landelijk en per school (Inspectie van het Onderwijs, 2024a, 2025; Langerak, 2025). Daarbij ligt de focus op de discrepantie met de ambitie dat 65% van de groep-8-leerlingen dit niveau zou moeten halen.

Kritische geluiden over het reken-wiskundeonderwijs (e.g., De Volkskrant, 2021) gaan ervan uit dat de metingen in peilonderzoeken en doorstroomtoetsen de feiten zijn. Er wordt dus stilzwijgend verondersteld dat het referentieniveau 1S gepaard gaat met een duidelijke en gefundeerde drempelwaarde, die goed gemeten wordt. Bovendien neemt men aan dat dergelijke metingen bruikbaar zijn om conclusies te trekken over het reken-wiskundeonderwijs. Oftewel: er worden uitspraken gedaan over de kwaliteit van het reken-wiskundeonderwijs, zonder stil te staan bij de vraag of genoemde veronderstellingen wel kloppen.

Buijs (2025) betoogt dat verklaringen voor de lage percentages leerlingen die 1S halen óók in de referentieniveaus en de metingen zelf gezocht moeten worden. Nu er veel wordt geschreven over de problemen in het onderwijs en er actieplannen worden geformuleerd, is het belangrijk dat niet alleen maatschappelijke en onderwijsinterne uitdagingen worden meegewogen, maar ook de manieren waarop leerresultaten worden gemeten en hoe die doorwerken in beleid en opinievorming (zie ook Heij, 2021).

In dit artikel presenteren we een probleemanalyse, waarbij we genoemde veronderstellingen rond het streefniveau 1S tegen het licht houden. Er staat immers veel op het spel voor stakeholders zoals leerlingen, leerkrachten, ouders, schoolleiders, toezichthouders, overheidsinstellingen en commerciële partijen. Met deze analyse willen we beter begrijpen waarom al sinds de invoering van de referentieniveaus 15 jaar geleden de percentages leerlingen die 1S op de rekentoetsen halen, achterblijven bij de door de overheid gestelde ambities (65% van de leerlingen zou 1S moeten halen). Ligt dat aan het rekenniveau, de toetsen of de gehanteerde drempelwaardes, of is er een mismatch tussen doelen, meetinstrumenten en gebruik van toetsresultaten?

Deze focus op de afstemming van al deze zaken is ingegeven door oude inzichten uit de onderwijswetenschappen. Cronbach (1971) bepleitte al: zorg dat doel, meetinstrument, drempelwaarden, gebruik van het instrument en de interpretatie van de verkregen data goed op elkaar zijn afgestemd. Alleen dan kan van een valide toetsprocedure worden gesproken, die adequate interpretaties van de resultaten mogelijk maakt. Vervolgens kan zorgvuldig worden afgewogen hoeveel belang er aan de resultaten gehecht kan worden in het licht van welk doel. Toetsresultaten kunnen immers erg informatief zijn, mits goed gebruikt.

Daartegenover staat de wet van Campbell (1979): ‘The more any quantitative social indicator is used for social decision-making, the more subject it will be to corruption pressures and the more apt it will be to distort and corrupt the social processes it is intended to monitor’ (p. 85; zie Heij, 2021, of een uitleg door Ehren in de podcastserie Over Sturing). Hoe meer ervan afhangt, zoals bij doorstroomtoetsen, hoe groter de kans dat de nadruk op leerresultaten leidt tot versmalling van het curriculum en teaching to the test (Madaus & Russell, 2017; Popham, 2001).

We willen benadrukken dat we niet proberen om tegenvallende resultaten weg te poetsen. We menen dat het reken-wiskundeonderwijs op veel scholen beter kan en moet, maar daarvoor is wel een grondige probleemanalyse nodig die de huidige manieren van meten en interpreteren meeneemt als mogelijk onderdeel van de problemen die worden ervaren in het reken-wiskundeonderwijs.

We starten met een korte toelichting op de doelen van de referentieniveaus en de resultaten met de huidige toetsprocedures. Vervolgens gaan we in op het meten van het streefniveau 1S aan de hand van een dichotome drempelwaarde. Daarna bespreken we het gebruik van de cijfers uit toetsen voor het evalueren van het reken-wiskundeonderwijs. Tot slot gaan we in op de haalbaarheid van de geformuleerde ambities op landelijk niveau.

 

Referentiekader: doelen, niveaus en toetsresultaten

 

Doelen

Het referentiekader (Expertgroep, 2008a) is ontwikkeld in opdracht van het Ministerie van Onderwijs, Cultuur en Wetenschap. Het doel was om te beschrijven wat leerlingen moeten kennen en kunnen op het gebied van taal en rekenen-wiskunde bij de verschillende onderwijsovergangen van primair tot hoger onderwijs, zodat de verschillende onderwijssectoren konden werken aan doorlopende leerlijnen. In de nadere doelformulering staat:

 

‘[Er moesten] ‘doorlopende leerlijnen’ [komen] die ervoor zorgen dat het onderwijsresultaat van de ene sector naadloos aansluit op dat van de andere, en ‘referentieniveaus’ met beschrijvingen van kennis en vaardigheden die leraren houvast bieden voor het bepalen, volgen en stimuleren van de ontwikkeling van leerlingen.’ (Expertgroep, 2008a, p. 7)

 

Uit het vervolgrapport, ‘Een Nadere Beschouwing’ (Expertgroep, 2009a), blijkt dat het referentiekader het midden houdt tussen een leerplankader (kerndoelen en eindtermen) enerzijds en toetsing anderzijds. Het referentiekader was ‘nadrukkelijk geen onderwijsprogramma en ook geen examenprogramma. Het referentiekader doet geen uitspraken over individuele leerlingen, maar is een ijkingsinstrument voor het onderwijssysteem als geheel’ (p. 6). Ook de Onderwijsraad (2011) schreef destijds dat de referentieniveaus een diagnostische functie moesten hebben tijdens het schooljaar, los van de afsluitende toetsen.

De commissie onder voorzitterschap van Meijerink heeft twee voorlopige referentieniveaus voorgesteld, met de bedoeling om via pilots en afstemming tussen de onderwijssectoren over een langere periode te komen tot doorlopende leerlijnen:

 

‘Het referentiekader ligt er nu en zal de komende jaren geleidelijk aan vertaald worden naar de verschillende onderwijssectoren. Dan wordt ook preciezer duidelijk welk niveau voor welke leerling zal gaan gelden.’ (Expertgroep, 2009b, p. 6)

 

Maar het liep anders. Zoals Meijerink in een interview met Ros (2014) zei, werd het een haastklus en is te snel tot wettelijke vastlegging overgegaan.

 

Fundamenteel en streefniveau voor rekenen

Het referentiekader voor rekenen werkt met vier domeinen (getallen, verhoudingen, meten en meetkunde, verbanden), drie onderdelen (notatie, taal en betekenis; met elkaar in verband brengen; gebruiken) en drie verschillende typen kennis en vaardigheden (paraat hebben, functioneel gebruiken, weten waarom).

Het referentiekader maakt een onderscheid tussen een ‘fundamentele kwaliteit’ F en een ‘streefkwaliteit’ S (Expertgroep, 2008b, p. 5). In de originele uitleg staat:

 

‘De streefkwaliteit van dit niveau (1S) omvat de onderdelen uit de fundamentele kwaliteit (1F) en is ten opzichte hiervan een verdieping van de kennis en vaardigheden. Deze verdieping kenmerkt zich doordat (wiskundig) redeneren, formaliseren en generaliseren (‘weten waarom’) verweven wordt met de onderdelen die ook op 1F voorkomen.’ (p. 36)

 

De Expertgroep doorlopende leerlijnen taal en rekenen (2008b) had voor deze twee referentieniveaus de volgende ambities geformuleerd voor het einde van de basisschool:

• het percentage leerlingen dat minimaal niveau 1F haalt moet toenemen van 75% naar 85%;
• het percentage leerlingen dat minimaal niveau 1S haalt moet toenemen van 50% naar 65%.

De lagere percentages waren schattingen van de toenmalige situatie (75% en 50%). De streefpercentages waren bedoeld als stippen op de horizon, geen normen waar de populatie, laat staan individuele scholen aan moesten voldoen. Overigens bleek de ambitie van 85% 1F al te worden gehaald bij invoering van de referentieniveaus, en was dit niveau dus feitelijk geen ambitie.

 

Toetsresultaten en beheersing referentieniveaus

Of leerlingen aan het eind van de basisschool de referentieniveaus 1F of 1S halen bij rekenen-wiskunde wordt momenteel op basis van twee verschillende typen toetsen vastgesteld. Enerzijds hebben we landelijke peilingsonderzoeken (voorheen PPON, tegenwoordig Peil.Rekenen-Wiskunde), anderzijds de doorstroomtoetsen (voorheen eindtoetsen). Het doel van peilingsonderzoeken is om een indruk te krijgen van de landelijke situatie, op basis van een grote, representatieve steekproef. In het meest recente peilingsonderzoek haalde 84% van de leerlingen uit het reguliere basisonderwijs 1F en 33% haalde 1S (Inspectie van het Onderwijs, 2024a).

Deze peilingsonderzoeken zijn niet heel informatief omdat het om low stakes toetsen gaat: voor leerlingen hangt er niets van af. Daardoor vallen resultaten veel lager uit dan in high-stakes toetsen zoals de eindtoetsen en doorstroomtoetsen (voor onderzoek naar zogeheten differentiële motivatie zie Keizer-Mittelhaëuser, 2014). In Peil.Rekenen-Wiskunde 2019 kon dit verschil vrij precies ingeschat worden: in het peilingsonderzoek haalde 33% van de leerlingen 1S, terwijl van dezelfde groep leerlingen 48% niveau 1S haalde op de eindtoets (Inspectie van het Onderwijs, 2021).

Eindtoetsen en doorstroomtoetsen vormen dus een andere informatiebron om een beeld te krijgen van de leerresultaten. De percentages leerlingen die op deze toetsen 1F halen, schommelen sinds de invoering rond de 90%, terwijl de percentages leerlingen die 1S halen rond de 45% liggen (Buijs, 2024).

 

Streefniveau 1S als drempelwaarde

We hebben gemerkt dat het lastig is om te communiceren over de referentieniveaus. Een voorbeeld hiervan is de ambiguïteit van 1F en 1S als drempelwaardes of intervallen. Als drempelwaardes zijn ze punten op een vaardigheidsschaal: een leerling kan links of rechts van de drempel 1F of 1S scoren (bovenste situatie in afbeelding 1). Maar in de rapportages van de inspectie worden ze als intervallen gerapporteerd (een bepaald percentage leerlingen heeft 1F behaald (middelste situatie in afbeelding 1). In het geval van 1F is er de extra complicatie dat 1F soms als alleen als interval tot 1S wordt opgevat (dus wel 1F maar niet 1S halen) en soms als alles vanaf 1F (dus minstens 1F halen, ook wel genoteerd als >1F of ≥1F, zie de onderste situatie in afbeelding 1). Merk verder op dat de plaatjes in leerlingvolgsystemen (bijvoorbeeld van ‘Leerling in Beeld’) er weer anders uitzien, namelijk een gekleurde balk tot aan de behaalde score in een interval. De reden hiervoor is dat in leerlingvolgsystemen een gekleurde balk de score van een individuele leerling representeert, niet het percentage leerlingen dat een bepaald niveau haalt.

 

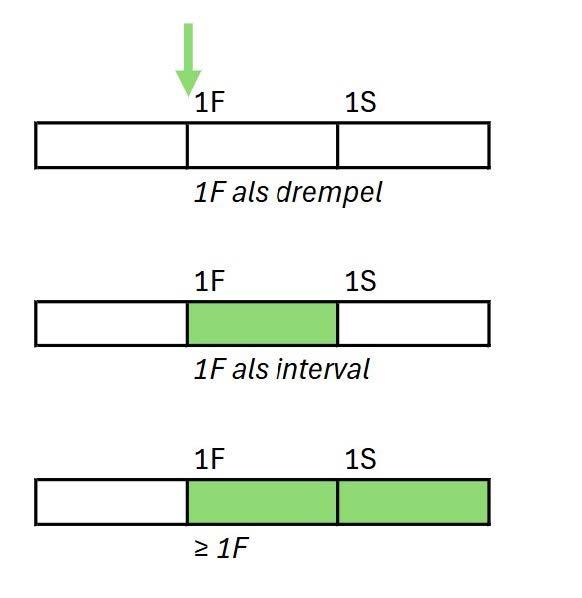
Validiteit van 1S als drempelwaarde

Rekenen-wiskunde is een complex terrein dat meestal wordt onderverdeeld in verschillende samenhangende domeinen. Het referentiekader, met de verschillende domeinen, onderdelen en typen kennis, sluit daarbij aan. Zowel referentieniveau 1F als 1S beslaat dus een breed spectrum van kennis, vaardigheden en inzichten.

Bij het meten van die niveaus in peilingsonderzoek en in eind- en doorstroomtoetsen zijn ze echter punten op een vaardigheidsschaal geworden (drempelwaarden). 1S is hiermee niet meer verbonden aan álle onderdelen die een leerling moet beheersen volgens de inhoudelijke beschrijving van vaardigheden (kennen, kunnen en weten waarom) uit het referentiekader. Daardoor laat een toetsresultaat niet meer zien of een leerling werkelijk alle onderdelen van 1S beheerst. Dit laatste heet inhoudsvaliditeit en die is door de keuze van één score op één schaal slecht onderbouwd. Dit geldt overigens ook voor de peilingsonderzoeken (Gravemeijer & Van Galen, 2023).

Een tweede bedreiging van de validiteit betreft het uitgangspunt dat 1S beschrijft wat nodig is voor doorstroom naar vmbo-tl, havo en vwo. Harskamp zette in het hoofdrapport van de Expertgroep (2008a) al vraagtekens bij de voorspellende waarde van de standaarden voor het vervolgonderwijs. Bij ons weten is er nooit gedegen empirisch onderzoek gedaan naar die voorspellende waarde en de vereiste aansluiting op het voortgezet onderwijs. Geluiden uit de praktijk zijn dat 1S als voorwaardelijk wordt gezien voor havo en vwo, maar slechts voor een deel van de leerlingen met een vmbo-tl-advies. Vmbo-tl-leerlingen hebben immers nog ongeveer drie jaar om niveau 2F te bereiken. Het is dus onduidelijk hoe goed de drempelwaarde van 1S is afgestemd op het vervolgonderwijs, waarmee ook de criteriumvaliditeit wankel is.

Als we deze twee beperkingen in de validiteit van 1S samennemen, moeten we concluderen dat referentieniveau 1S met de bijbehorende drempelwaarde niet goed gefundeerd is. Uit het rapport van het meest recente peilingsonderzoek voor rekenen-wiskunde (Inspectie van het Onderwijs, 2024a) blijkt dat ook een focusgroep van experts hun twijfels had. Leden van die focusgroep uitten toen ook zorgen over de validiteit en het gebruik van de referentieniveaus:

 

‘Met de behaalde referentieniveaus 1F en 1S kon de focusgroep niet zoveel. Deze niveaus vindt zij niet goed doordacht. Het ministerie volgde destijds niet alle adviezen van de ontwikkelgroep en stuurde bovendien niet op niveau 1S.’ (p. 21)

 

Meer algemeen zetten sommige deelnemers aan de discussie vraagtekens bij de referentieniveaus als graadmeter. Dit geldt eveneens voor de bijbehorende ambities die de commissie-Meijerink formuleerde. Bij het beoordelen van de resultaten van deze peiling moeten deze referentieniveaus niet leidend zijn, vinden deelnemers. (p. 22)

Een van de leden zei:

 

‘De expertgroep die betrokken was bij de bepaling van de referentieniveaus dacht destijds dat bewerking met breuken op niveau 2S zou moeten staan. Maar dit item is uiteindelijk bij niveau 1F terechtgekomen. Daarnaast stelt Cito bij de beoordeling van toetsresultaten op grond van schaling vast of je 1F of 1S hebt gehaald. Dat is niet 1 op 1 hetzelfde als de omschrijving van de inhoud van niveau 1F of 1S. […] Je kunt je afvragen of 1S voor het geambieerde percentage leerlingen haalbaar is. Dat is nooit empirisch vastgesteld.’ (p. 24)

 

In het rekenrapport van de Expertgroep staat inderdaad bij ‘bewerkingen met breuken op papier uitvoeren’ vermeld dat dit ‘vanaf 2S’ is (2008b, p. 38; zie ook Van den Broek et al., 2022). Dat er zulke uiteenlopende ideeën zijn over waar een specifieke leerinhoud bij hoort illustreert de problemen met de inhoudsvaliditeit van 1S.

Samenvattend zijn er verschillende redenen waarom we concluderen dat 1S als drempelwaarde onvoldoende gefundeerd is. Een beschrijving van een referentieniveau als 1S op basis van de inhoud en op basis van schaling is niet hetzelfde. En omdat we uitgaan van één algemene vaardigheidsschaal voor rekenen is het maar de vraag of de koppeling met de inhoud stand houdt. Als een leerling niveau 1S haalt, is dat dan op alle inhoudelijke onderdelen die onder 1S beschreven staan? Een dichotome drempelwaarde kan geen recht doen aan de inhoudelijke complexiteit en diversiteit in reken-wiskundedomeinen. Een laatste belangrijk punt is dat er geen ijking heeft plaatsgevonden om vast te stellen of de inhoudelijke beschrijving daadwerkelijk aansluit bij wat in het voortgezet onderwijs nodig is, waardoor we niet weten of de drempelwaarde wel op de goede plek is neergelegd.

 

Kunnen we 1S betrouwbaar meten?

Niet alleen is de drempelwaarde van 1S onvoldoende gefundeerd, de cijfers die we nu gebruiken uit de doorstroomtoetsen blijken onbetrouwbaar te zijn. Er zijn grote verschillen tussen doorstroomtoetsen in percentages 1F en 1S/2F, zowel bij rekenen als bij taal (afbeelding 2, CvTE, 2025). Bij Route 8 haalde 25,3% van de leerlingen 1S voor rekenen, terwijl dat bij Lib (Leerling in beeld) op papier 48,5% was. Dat is ruim 23 procentpunt verschil, of anders gezegd: bijna twee keer zo veel.

 

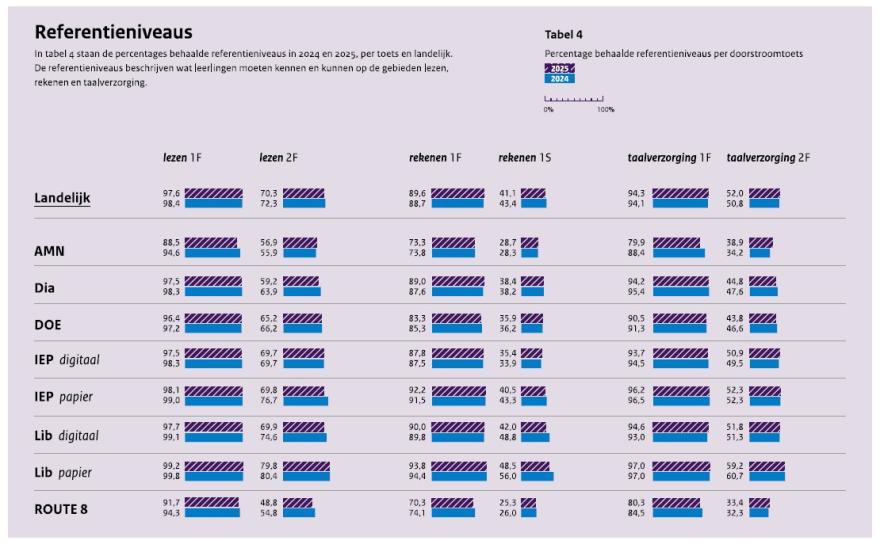
Een van de vele mogelijke verklaringen voor de verschillen is dat de huidige strategie om cesuren te bepalen is verouderd. In een recente audit van de doorstroomtoetsen schrijft Van Rijn (2025): ‘De huidige cesuren voor de toetsadviezen zijn gebaseerd op eindtoetsgegevens uit 2015 en die voor de referentieniveaus zijn afkomstig uit de centrale eindtoets 2018’ (p. 28). Er is dus behoefte aan een ‘verversingsstrategie’ (p. 28).

Als verklaring voor de verschillende uitkomsten is ook wel gesuggereerd dat scholen toetsen kiezen die bij hun leerlingpopulatie passen. Het CvTE (2025) wijst hierop: ‘Zo zijn er aanwijzingen dat scholen met een minder vaardige leerlingpopulatie eerder voor een adaptieve toets kiezen om de leerlingen niet te overvragen’ (p. 3). Een onderzoek van De Volkskrant (Meindertsma et al., 2025) toont echter aan dat de verschillen tussen de toetsen niet met schoolweging verklaard kunnen worden. Immers de verschillen zijn over de hele linie van schoolweging ongeveer even groot. Bovendien laat een recente analyse van de PO-Raad (2025a) zien dat scholen die zijn overgestapt naar ‘makkelijkere toetsen’ in 2025 veel beter scoorden. Het lijkt er dus wel degelijk op dat de toetsen niet gelijkwaardig zijn. Dat levert op populatieniveau onbetrouwbare scores op, wat op zichzelf al onwenselijk is. Nog zorgelijker is echter dat individuele scholen worden beoordeeld op deze onbetrouwbare cijfers, niet alleen door de inspectie, maar ook door colleges van bestuur, toezichthouders en ouders.

 

Gebruik van de referentieniveaus op schoolniveau

Zoals eerder beschreven was het referentiekader niet bedoeld voor uitspraken over individuele scholen (Expertgroep, 2009b). Ook in 2023 stelde toenmalig minister Wiersma (2023) in een brief over het masterplan basisvaardigheden: ‘Wel wil ik opmerken dat beleidsdoelen geen doelen zijn voor individuele scholen’ (p. 7). Toch is dat precies wat er nu gebeurt vanwege de wettelijke invoering van het referentiekader (Hooge, 2014). Voor elke basisschool berekent de inspectie jaarlijks op basis van de eindtoetsen (vanaf 2023–2024 de Doorstroomtoets) of het 3-jaarsgemiddelde van de leerresultaten voldoende of onvoldoende is (Inspectie van het Onderwijs, 2024b). Op de website https://scholenopdekaart.nl kan iedereen open data van elke school inzien. De inspectie rapporteert verder signaleringswaarden voor de percentages leerlingen die de referentieniveaus voor rekenen en taal halen (1F en 1S/2F), afhankelijk van de schoolweging, op 1 decimaal nauwkeurig (afbeelding 3). De inspectie beoordeelt de leerresultaten van een school als onvoldoende als de behaalde percentages voor een of beide indicatoren van de referentieniveaus 1F en 1S/2F onder de signaleringswaarde liggen, al kan de verantwoording van de school daar nog wat aan veranderen.

 

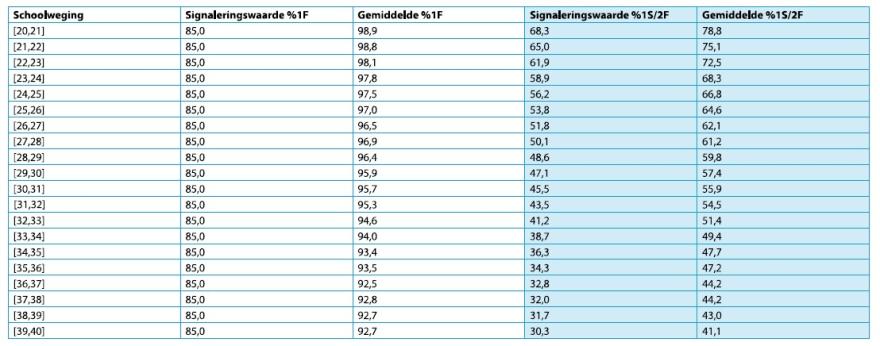
Ambities voor dichotome drempelwaarden, bedoeld om iets over een populatie te zeggen, zijn echter ongeschikt om op steekproefniveau te hanteren (een groep 8 van een willekeurige school). Een gedachten-experiment kan dit verhelderen. Stel dat een populatie (alle groep-8-leerlingen in het land) voldoet aan de gestelde ambitie dat 65% van de leerlingen 1S haalt. Stel dat we random steekproeven nemen van groep-8-leerlingen (scholen). Ongeacht het aantal steekproeven (scholen) en hun omvang kunnen we verwachten dat in bijna de helft van de scholen minder dan 65% van de leerlingen 1S haalt (centrale limietstelling). Oftewel: bijna de helft van de scholen voldoet niet aan de norm, terwijl toch de populatie als geheel in orde is. Als illustratie hebben we in afbeelding 4 gekozen voor 6000 scholen met gemiddeld 30 groep-8-leerlingen.

 

Afbeelding 4. Simulatie van een serie van 6000 steekproeven (scholen) met n = 30 (groep-8-leerlingen) uit een hypothetische populatie waarin 65% van de leerlingen 1S of hoger haalt (proportie succes p = 0,65); de steekproevenverdeling is normaal verdeeld met een gemiddelde van 65%. Bron: https://stats.cpm.org/propsamples/

 

Natuurlijk is de werkelijke situatie complexer. Leerlingen zijn niet random over scholen verspreid, scholen verschillen, het aantal leerlingen in groep 8 varieert per school. Maar dit voorbeeld laat wel zien dat populaties andere kenmerken kunnen hebben dan steekproeven. De analyse van Langerak (2025) van het aantal keer dat scholen in vier opeenvolgende schooljaren ‘1S-niveau behalen’ (oftewel, dat 65% van de leerlingen 1S haalt) houdt daar geen rekening mee en schept daarmee een misleidend beeld van de situatie.

Wat we in de praktijk zien, is dat de inspectie lagere percentages hanteert (afbeelding 3) dan toezichthouders van colleges van bestuur en schoolbesturen zelf. Ook zien we regelmatig dat van leerkrachten in groep 8 wordt verwacht dat ze bepaalde percentages behalen; soms zelfs veel hoger dan 65% 1S. Dit kan doorwerken in hoe leerkrachten hun onderwijs vormgeven (risico van teaching to the test), en hoe ze met hun leerlingen en ouders over het rekenniveau praten.

Los van de misleidende vertekening door landelijke streefpercentages op scholen toe te passen, kleven er ook pedagogische nadelen aan de nadruk op drempelwaarden. Het kan leerling en leerkracht demotiveren als een bepaalde drempel ondanks alle inspanningen niet wordt gehaald. Leerlingen kunnen al vroeg een lage zelfcompetentie ontwikkelen als ze te vaak of expliciet worden vergeleken met een drempel of met anderen. Het niet voldoen aan de verwachtingen leidt vaak tot een lage rekenbeleving, die het leren rekenen aanzienlijk belemmert (Timmerman et al., 2017). En voor de leerlingen die in groep 7 het streefniveau al hebben gehaald, valt de druk om door te groeien weg, in ieder geval tot de doorstroomtoets. 1S biedt geen stimulans voor leerlingen die in principe in staat zijn om abstractere wiskunde te leren (Harskamp in bijlage A van Expertgroep doorlopende leerlijnen taal en rekenen, 2008b). De expertgroep had naast 1F en 1S ook een hogere drempel aangeraden maar dat advies is niet opgevolgd (zie ook Sjoers, 2013). De nadruk op het halen van twee specifieke drempelwaardes kan dus afleiden van het zicht op de individuele mogelijkheden van leerlingen. Dat is niet alleen onwenselijk voor leerlingen die moeite hebben met rekenen, maar ook voor leerlingen die veel meer zouden kunnen. Een systeem met meer nadruk op vaardigheidsscores, in plaats van de drempels, maakt het makkelijker om per leerling of school groei te stimuleren binnen de zone van naaste ontwikkeling.

 

Inconsistenties tussen de referentieniveaus rekenen en taal

In deze paragraaf maken we een vergelijking tussen de referentieniveaus bij rekenen en bij taal, een andere basisvaardigheid die centraal staat in maatschappelijke discussies. Allereerst bestaat er geen 1S-niveau voor taal; daar wordt 2F gehanteerd als tweede niveau voor het basisonderwijs (Besluit referentieniveaus Nederlandse taal en rekenen, 2010). De werkgroepen rekenen en taal werkten onafhankelijk en de Expertgroep (2008a) heeft oorspronkelijk geen ambities voor het percentage 1F en 2F geformuleerd voor taal. Toch gebruiken instanties als de inspectie (bijvoorbeeld Inspectie van het Onderwijs, 2024a; 2024b) en SLO (bijvoorbeeld 2024) wel streefpercentages. Met 85% voor 1F en 65% voor 2F zijn de ambities voor de referentieniveaus van taal hetzelfde als die voor 1F en 1S bij rekenen.

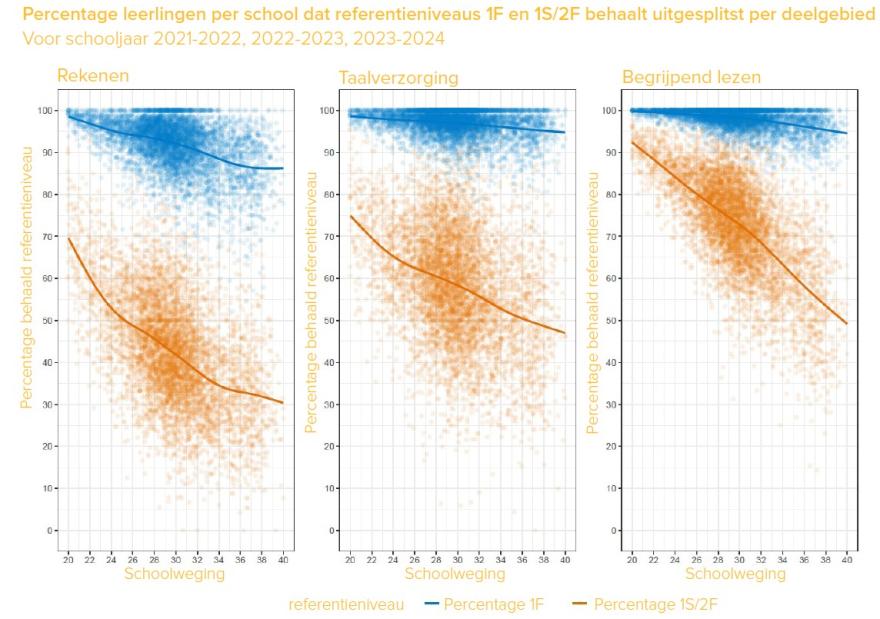
Wat opvalt sinds de invoering van het referentiekader is dat veel meer leerlingen het 2F-niveau halen op de taaltoetsen dan het 1S-niveau op de rekentoetsen (afbeelding 5, zie ook afbeelding 2). Het is echter niet aannemelijk dat Nederlandse leerlingen veel beter zijn in taal dan in rekenen, als we naar internationale toetsresultaten kijken. Immers, als we TIMSS (rekenen) en PIRLS (taal) vergelijken, dan blijkt dat Nederland bij TIMSS ruim boven het gemiddelde scoort (537) en op nummer 13 staat (van 58 landen) (Meelissen et al., 2024) en bij PIRLS op plek 18 van 43 landen, met een score (527) net onder het gemiddelde van de 21 Westerse landen die meededen (Swart et al., 2023). Dat wijst erop dat de 1S-lat voor rekenen relatief hoger ligt dan de 2F-lat bij taal. En dat is op zich niet vreemd: die referentieniveaus zijn oorspronkelijk ook niet ontwikkeld om ‘hetzelfde niveau’ bij taal en rekenen aan te geven. Het is daarmee onwenselijk dat toezichthouders de resultaten voor taal en rekenen op dezelfde manier vaststellen en ijken (2F bij taal en 1S bij rekenen, met voor beide streefpercentages van 65%), en op basis van de vergelijking conclusies over de opbrengsten van het taal- en reken-wiskundeonderwijs trekken. Dergelijke inconsistenties zijn overigens goed gedocumenteerd (Van den Broek et al., 2022) en door het Ministerie van Onderwijs, Cultuur en Wetenschap onderkend (2024).

 

Conclusies en aanbevelingen

De aanleiding voor dit artikel was dat de discussie over de kwaliteit van het reken-wiskundeonderwijs vooral gevoerd wordt op basis van een erg smalle opvatting van kwaliteit, namelijk de percentages van groep-8-leerlingen die 1S halen. Een breed inhoudelijk kader wordt zo teruggebracht tot één specifieke meetwaarde op een vaardigheidsschaal, waarbij er bovendien grote zorgen over de betrouwbaarheid van de metingen bestaan. Onze analyse, maar ook die van Buijs (2025), wijst op de ernstige tekortkomingen van 1S als maatstaf voor het succes van het reken-wiskundeonderwijs. Vandaar onze oproep: reken het reken-wiskundeonderwijs niet af op percentages leerlingen die 1S halen.

 

Er zijn goede redenen om de referentieniveaus voor rekenen grondig te herzien of zelfs af te schaffen. Samengevat:

1. De referentieniveaus zijn nooit bedoeld om te worden gebruikt zoals ze nu worden ingezet (Expertgroep, 2008a; 2008b; Ros, 2014) en ze zijn ook niet geschikt voor de beoordeling van scholen.
2. De inhouds- en criteriumvaliditeit van de meting van het streefniveau 1S zijn onvoldoende. De operationalisatie van 1S als punt op een rekenvaardigheidsschaal doet onvoldoende recht aan de inhouden zoals in het referentiekader worden beschreven. De aanname dat niveau 1S nodig is voor doorstroom naar vmbo-tl is niet onderbouwd.
3. Doordat de doorstroomtoetsen onderling onvergelijkbaar zijn (PO-Raad, 2025a), zijn de cijfers over beheersing van 1S niet betrouwbaar. De invoering van één doorstroomtoets zou weliswaar deze oneerlijke verschillen voorkomen, maar neemt het diepere validiteitsprobleem niet weg (nog los van de vraag of vroege selectie wenselijk is; Onderwijsraad, 2021).
4. In de huidige rapportage en evaluatie van onderwijsresultaten zijn de referentieniveaus 1F en 1S te centraal komen te staan. Het werken met dichotome indelingen – zoals het al dan niet behalen van 1S – heeft te veel nadelen. Cesuren (drempelwaardes) die op populatieniveau worden gesteld, zijn ongeschikt om op steekproeven (scholen) toe te passen. Statistisch gezien zijn cesuren niet robuust; drempelwaarden zijn namelijk gevoelig voor variatie in het meetinstrument (zoals gebruikt in Peil.Rekenen-Wiskunde). Bovendien gaat er veel informatie verloren als je alleen het percentage tot een bepaalde cesuur rapporteert in plaats van een gemiddelde en spreidingsmaten. Nationale toetsing kan een voorbeeld nemen aan TIMSS en PISA die gemiddeldes en verschillende percentielen rapporteren (Meelissen et al., 2023; 2024).
5. Het noemen van een streefpercentage zonder sterke en gevalideerde onderbouwing en onderzoek naar de haalbaarheid, is onverstandig. De beoogde nationale verschuivingen vanaf de huidige 33% (peilonderzoek) of 46% (doorstroomtoetsen) naar de geambieerde 65% zijn niet realistisch. Op kleine schaal zijn aanzienlijke verbeteringen mogelijk, maar voorbeelden van dergelijke enorme verschuivingen op nationale schaal zijn ongekend. Schattingen op basis van effectgroottes kunnen een grove indicatie geven van hoe groot zulke verschuivingen zijn, maar wij hebben daarvan afgezien vanwege de eerdergenoemde validiteitsproblemen van referentieniveau 1S.

Uit bovengenoemde punten blijkt dat de huidige situatie ongewenst en oneerlijk is. De overheid zou de moed moeten hebben om de meetproblemen rond het referentieniveau 1S niet alleen te onderkennen (zie Ministerie van Onderwijs, Cultuur en Wetenschap, 2024; Van den Broek et al., 2022), maar ook om deze op korte termijn aan te pakken. Het risico is anders groot dat beleidsmaatregelen worden genomen die niet op een gedegen probleemanalyse zijn gebaseerd. Een goede probleemanalyse kijkt niet alleen naar brede maatschappelijke en onderwijsinterne factoren die het onderwijs onder druk zetten, maar ook naar de validiteit en betrouwbaarheid van de conclusies die voortvloeien uit een toetssysteem dat niet naar behoren functioneert.

Belangrijke factoren die we in dit artikel niet analyseren, maar die wel samenhangen met de prestaties van leerlingen en scholen, zijn onder andere het ongelijk verdeelde lerarentekort, het tekort aan schoolleiders, kansen(on)gelijkheid in relatie tot bijvoorbeeld de sociaaleconomische achtergrond van ouders en de verdere vakdidactische professionalisering van leerkrachten; niet alleen in de inductiefase maar ook daarna. De overheid heeft daar – via beleid – invloed op en datzelfde geldt ten dele ook voor schoolbesturen. Anders geformuleerd: aan de noodzakelijke voorwaarden voor het verzorgen van goed onderwijs is niet altijd voldaan.

Met onze kritiek lopen we het risico dat we verkeerd worden begrepen. We benoemen expliciet twee mogelijke misvattingen. We willen niet suggereren dat het reken-wiskundeonderwijs niet beter zou kunnen of moeten, of dat het allemaal wel meevalt. Integendeel. Er zijn veel kwesties die nu onvoldoende aandacht krijgen, zoals het prestatieverschil tussen jongens en meiden dat groter geworden is (Meelissen et al., 2024) en maatschappelijke veranderingen die om andere rekenvaardigheden vragen van voorheen (Hoogland 2023; Wiskunde voor Morgen, n.d.). Onderzoek gericht op specifieke kwesties en regelmatige bijstelling van de doelen, zoals recent voor de conceptkerndoelen is gebeurd, blijven daarom belangrijk.

We willen ook niet suggereren dat we tegen een doorstroomtoets zouden zijn. Een goede toets is een waardevolle aanvulling op de inschatting van de leerkracht. Maar die toets (liefst geen commerciële) moet enkel worden gebruikt voor het ene doel waarvoor die is ontwikkeld en niet te veel gewicht krijgen. Zoals Veenman (2022) concludeert na een discussie tussen Meijer en Sijtsma (2022) en Heij (2022):

 

‘De bovenstaande reacties overziend, zijn wij het op één punt eens: de Eindtoets zou niet tevens moeten worden gebruikt als meetinstrument voor onderwijskwaliteit met alle perverterende gevolgen van dien. Daar ligt een verantwoordelijkheid voor overheid én scholen.’ (p. 62)

 

Het goede nieuws is dat de nieuwe kerndoelen rekenen-wiskunde definitief zijn opgeleverd en worden vastgelegd in de wet. Het Ministerie van OCW heeft opdracht gegeven om het referentiekader opnieuw te beschouwen. Laat dit een gunstig moment zijn om het hele proces van onderwijsdoelen tot toetsing, evaluatie en monitoring in samenhang te brengen. Gezien de geschiedenis van het referentiekader adviseren wij goed vooruit te denken en consistent te communiceren over wat er wel en niet met de evaluatiecriteria en toetsresultaten mag gebeuren.